Circunferência: Posições relativas

Na geometria, entender as posições relativas das circunferências é crucial. Elas podem ser tangentes interna ou externamente, se intersectar em dois ou mais pontos, ou ser completamente disjuntas. Essas relações desempenham um papel vital em problemas de geometria, engenharia e física.

POSIÇÕES RELATIVAS

ENTRE PONTO E CIRCUNFERÊNCIA

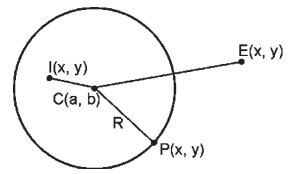
O ponto P(x, y) pertence à circunferência de centro C(a, b) e raio R se e somente se CP = R ⇔ (x − a)² + (y − b)² = R².
O ponto I(x, y) é interior à circunferência de centro C(a, b) e raio R se e somente se Cl < R ⇔ (x − a)²+(y−b)² < R² .
O ponto E(x, y) é exterior à circunferência de centro C(a, b) e raio R se e somente se CE > R ⇔ (x − a)² + (y − b)² >R² .

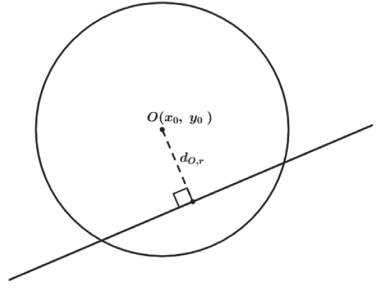
ENTRE RETA E CIRCUNFERÊNCIA

RETA EXTERIOR

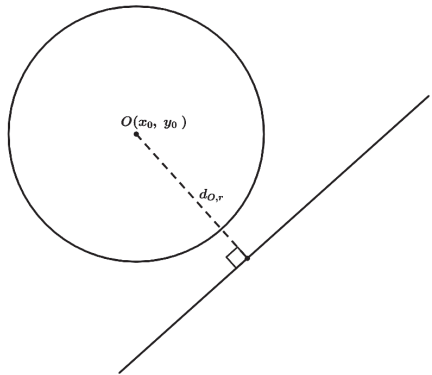
RETA TANGENTE

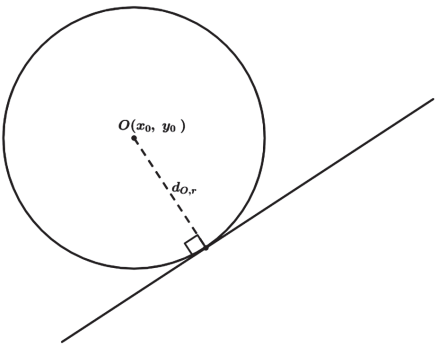
RETA SECANTE

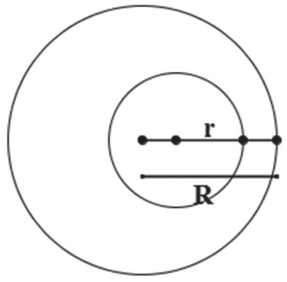
ENTRE DUAS CIRCUNFERÊNCIAS

EXTERIORES

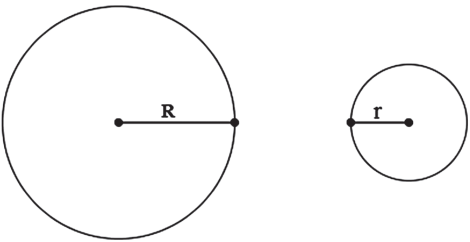
TANGENTES EXTERIORES

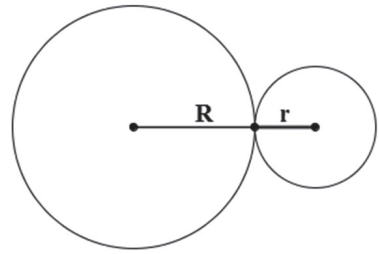
SECANTES

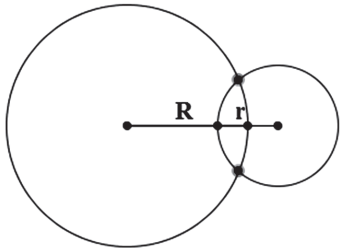
TANGENTES INTERIORES

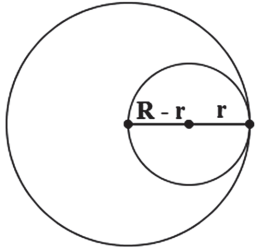
INTERIORES