DEFINIÇÃO
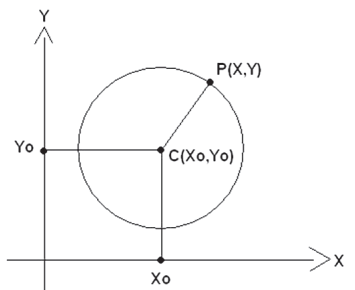
Utilizando a propriedade da circunferência como o lugar geométrico dos pontos do plano equidistantes de um único ponto teremos, P(x,y) como um ponto qualquer de raio R e O(x0,y0).

(x − x0)² + (y − y0)² = R² ⇒ Equação reduzida da circunferência
O(x0, y0) ⇒ Centro da circunferência
R ⇒ Raio da circunferência
Exemplo: a equação reduzida de uma circunferência de centro O(2, –3) e raio 4 é
(x−2)² +(y−(−3))² = 4² ⇒ (x−2)² + (y+3)² = 16
EQUAÇÃO COMPLETA
Desenvolvendo os produtos notáveis da equação reduzida teremos Ax² + Ay² + Bx + Cy + D = 0, onde para voltarmos para equação reduzida, para se determinar o centro e o raio devemos fazer o processo de completar quadrados, mas antes iremos fazer o reconhecimento de uma equação de circunferência.
Ax² + By² + Cx + Dy + Exy + F=0
Esses são todos os elementos que uma cônica pode apresentar, para que essa equação represente uma circunferência devemos ter sempre

Ou seja x² e y² devem ter o mesmo coeficiente e não pode haver o termo xy.
Completando os quadrados da equação x² + y² − 4x + 6y −3 = 0 ⇒ x² + y² − 4x + 6y − 3 = 0 ⇒ x² − 4x + y²+ 6y − 3 = 0 ⇒ x² − 2 · 2x + y² + 2 · 3y − 3=0.
Nos produtos notáveis o 1º termo é x e o 2º termo é 2 e também o 1º termo é y e o 2º termo é 3, daí vamos acrescentar o quadrado do 2º termo em cada caso e ao mesmo tempo subtraí-lo, para não “desiquilibrar” a igualdade.

Também podemos fazer o seguinte, desde que a equação completa da circunferência possua os coeficientes de x² e y² iguais a 1 (caso não seja podemos dividir toda a equação pelo valor do coeficiente).

Exemplo: 2x² + 2y² + 6x − 8y − 15 = 0, teremos 2x² + 2y² + 6x − 8y − 15 = 0, 2 ⇒ x² +y² +3x − 4y − 15/2 = 0.





