CIRCUNFERÊNCIA
A circunferência é o lugar Geométrico dos pontos de um plano equidistante de um ponto fixo do mesmo plano, chamado de centro.
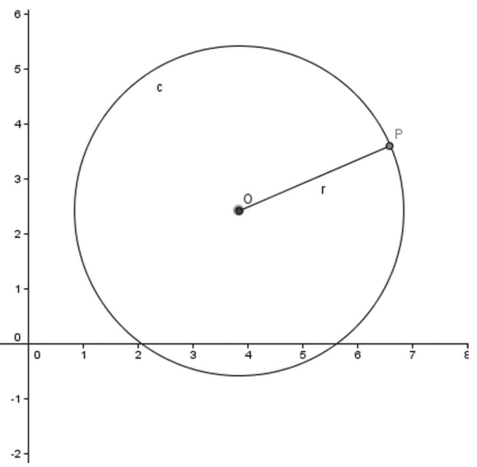
Seja a circunferência de centro O(x0, y0) e raio r e P um ponto qualquer (x, y).
Pela definição temos:

Substituindo r na equação acima e elevando ao quadrado (x − x0)2 + (y − y0)2 = r2. Que é a equação reduzida da circunferência. Desenvolvendo a equação reduzida temos:
x2 + y2 − 2x0x − 2y0y + x20 + y02 − r2 = 0
Fazendo −2x0 = D,−2y0 = E, x20 + y20 − r2 = F obtemos x2 + y2 + Dx + Ex + F = 0 (equação geral da circunferência) que é uma circunferência de centro:

Para que a equação x2+y2+Dx+Ex+F=0 represente uma circunferência devemos ter D2+E2−4F>0.
Exemplo:
Determine a equação da circunferência, sabendo-se que um de seus diâmetros é o segmento de extremos A(1, 3) e B(5, –3).
Resolução:
O ponto médio de AB é o centro C(3, 0) da circunferência e R2 = (3 − 1)2 + (0 − 3)2 ⇒ R2 = 13.
A equação da circunferência é (x − 3)2 + y2 = 13.
POTÊNCIA DE UM PONTO EM RELAÇÃO A UMA CIRCUNFERÊNCIA
Dados um ponto P(xp , yp) e uma circunferência (x − x0)2 + (y − y0)2 = R2, chamamos potência do ponto em relação à circunferência ao número real.
k = (xp − x0)2 + (yp − y0)2 − R2
A soma das duas primeiras parcelas representa o quadrado da distância do ponto P ao centro C da circunferência, então:
se k > 0 o ponto P é exterior;
se k = 0 o ponto P pertence à circunferência;
se k < 0 o ponto P é interior.
POSIÇÕES RELATIVAS ENTRE RETA E CIRCUNFERÊNCIA
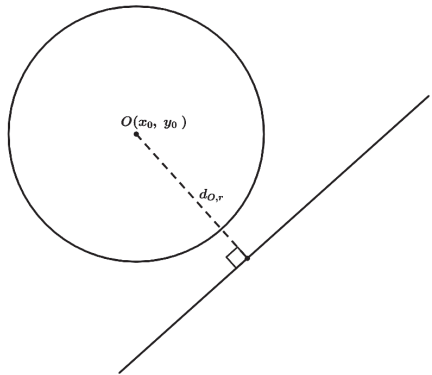
RETA EXTERIOR

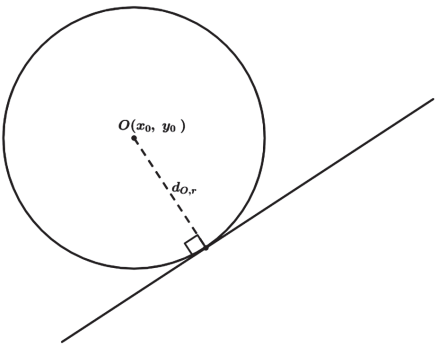
RETA TANGENTE

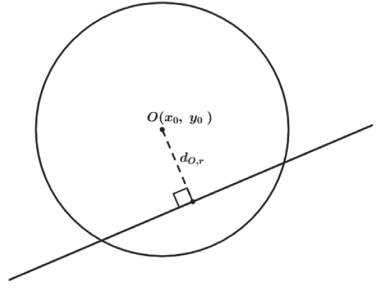
RETA SECANTE

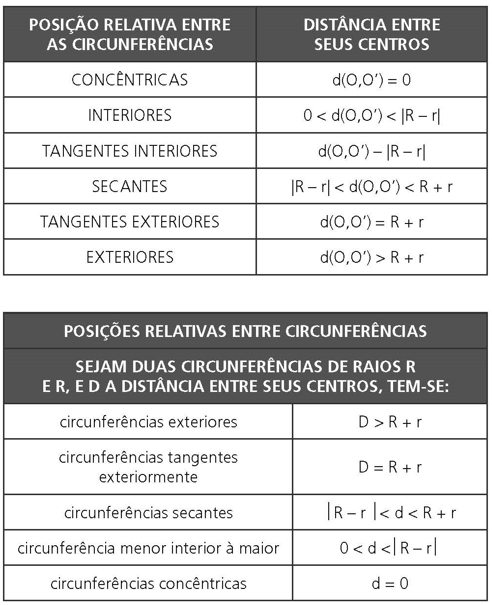
POSIÇÕES RELATIVAS ENTRE CIRCUNFERÊNCIAS
Sejam duas circunferências de centros O e O’, e raios r e R, respectivamente.
As circunferências são CONCÊNTRICAS se, e somente se, a distância entre seus centros for nula: d(O,O’) = 0.
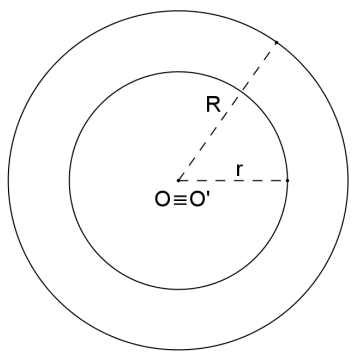
As circunferências são INTERIORES se, e somente se, a distância entre seus centros é maior do que zero e menor do que o módulo da diferença entre seus raios: 0 < d(O,O’) < |R – r|.
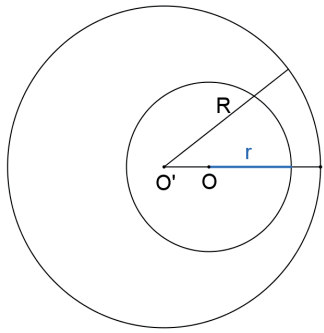
As circunferências são TANGENTES INTERIORES se, e somente se, a distância entre seus centros é igual ao módulo da diferença entre seus raios: d(O, O’) = |R – r|.
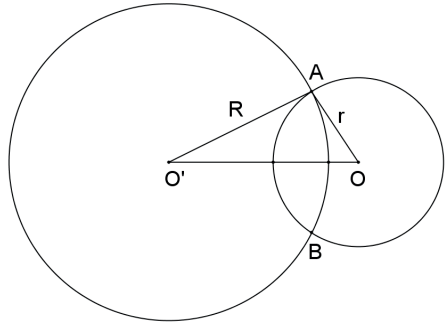
As circunferências são SECANTES se, e somente se, a distância entre seus centros é maior do que o módulo da diferença entre seus raios e menor do que a soma dos raios: |R – r| < d(O, O’) <R + r.
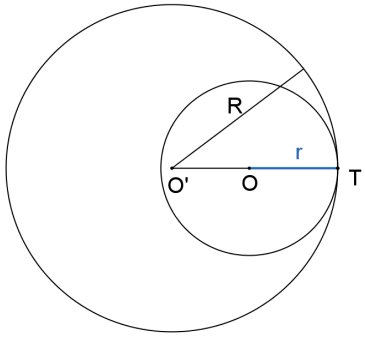
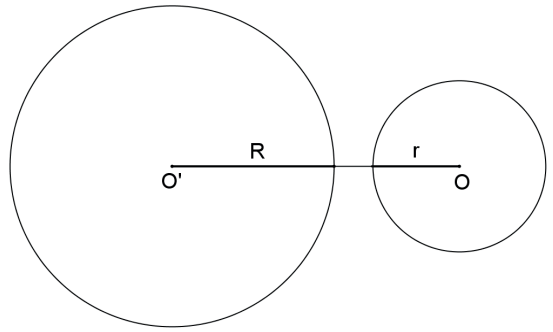
As circunferências são TANGENTES EXTERIORES se, e somente se, a distância entre seus centros é igual à soma dos raios: d(O, O’) = R + r.
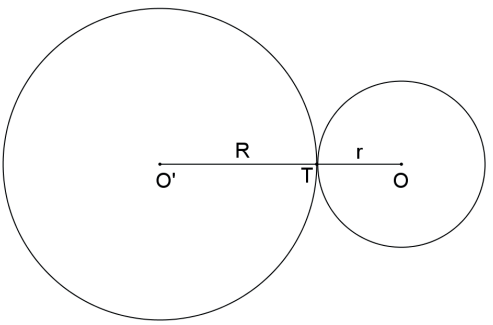
As circunferências são EXTERIORES se, e somente se, a distância entre seus centros é maior do que a soma dos raios: d(O, O’) > R + r.
RETA TANGENTE A CIRCUNFERÊNCIA
Sempre que desejamos encontrar a intersecção entre 2 curvas devemos resolver um sistema envolvendo as equações das 2 curvas. O sistema encontrado entre uma equação de circunferência e uma equação de reta seria:

Assim por substituição teremos:

Logicamente isso não foi exposto para ser decorado mas sim para mostrar que todo sistema entre uma equação de reta e uma equação de circunferência resulta numa equação do 2° grau onde daí sabemos que
Δ>0 → 2 pontos de intersecção → reta secante
Δ=0 → 1 ponto de intersecção → reta tangente
Δ<0 → Nenhum ponto de intersecção → reta exterior
Daí da equação (m2 + 1)x2 + (B + cm + 2mn)x + (n2 + cn + D) = 0 resultante do sistema basta fazermos o delta corresponde a situação de reta que nos for pedida.
Exemplo: Encontre a equação de reta que passa pelo ponto (-1, 0) e e é tangente a circunferência x2 + y2 − 12x + 20 = 0.
Reta y = mx + n que passa por (−1, 0) → 0 = m(−1) + n → m = n, assim y= mx + m.

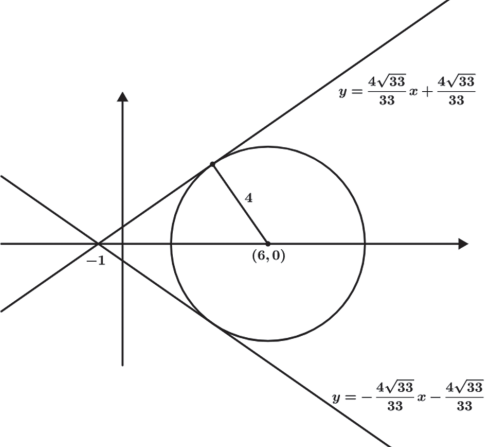
Também é possível encontrar a reta tangente utilizando a fórmula de distância de ponto a reta. Para isso devemos encontrar o centro e o raio da circunferência.

Centro (6, 0) e R2 = 16 ⇒ R = 4
A reta como vimos é y = mx + m ⇒ mx − y + m = 0.
Assim pela fórmula de distância de ponto a reta sendo a reta na sua forma completa e seus coeficientes a = m, b = -1 e c = m.

ONDIÇÕES PARA QUE UMA EQUAÇÃO DO 2º GRAU COM DUAS VARIÁVEIS REPRESENTE UMA CIRCUNFERÊNCIA
Procuremos as condições a que deve satisfazer a equação geral do 2º grau com duas variáveis, Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 para representar uma circunferência.
Concluímos que, dada uma equação do 2º grau com duas variáveis, as condições necessárias para que a mesma represente uma circunferência, no sistema cartesiano ortogonal, são:
A = C ≠ 0
B = 0
Respeitadas estas condições determinamos:





