VETOR DESLOCAMENTO
Seja a origem um ponto O arbitrariamente escolhido e uma partícula movendo-se em uma trajetória qualquer. O vetor posição de uma partícula em um instante t é o vetor de origem no ponto O e extremidade final no ponto onde se encontra a partícula.
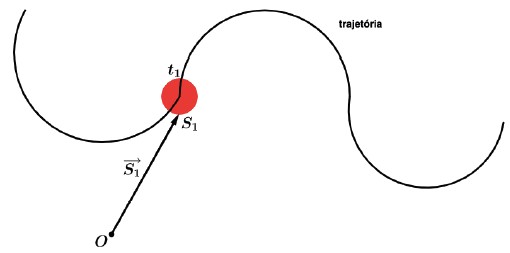
Sejam S1 e S2 as abscissas da partícula nos instantes t1 e t2, respectivamente (com t2 > t1), e sejam S1→ e S2→ os vetores posição da partícula nos mesmos instantes. Na Cinemática escalar definimos a variação de abscissa ∆S por ∆S = S2 – S1. Na Cinemática vetorial definimos o vetor deslocamento (d→) da partícula entre os instantes t1 e t2 por

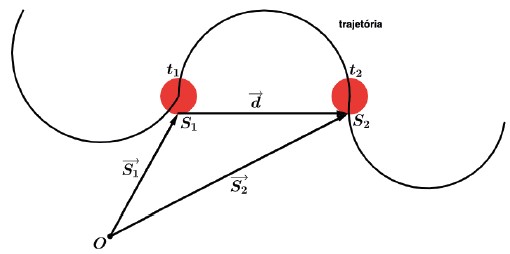
Observação: Quando a trajetória é retilínea temos:

O módulo da velocidade escalar média é maior ou igual ao módulo da velocidade vetorial média, num mesmo intervalo de tempo.

VELOCIDADE VETORIAL MÉDIA
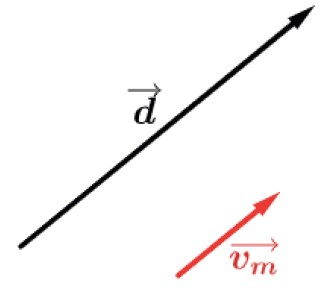
Na cinemática vetorial definimos como velocidade vetorial média por

O vetor vm→ possui a mesma direção e o mesmo sentido do vetor d→.
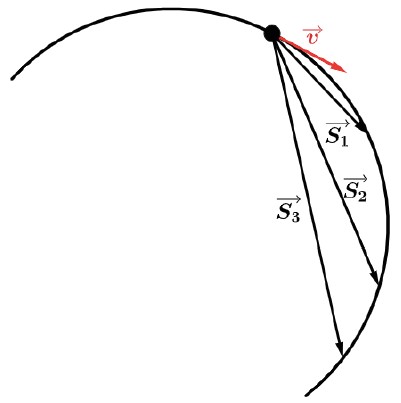
VELOCIDADE VETORIAL INSTANTÂNEA
A velocidade vetorial instantânea tem as seguintes características:
- Direção: mesma direção da reta tangente à trajetória no ponto considerado;
- Sentido: o mesmo do movimento;
- Módulo: igual ao módulo da velocidade escalar instantânea.
Observação:
Movimento retilíneo uniforme: Como a trajetória é retilínea, a velocidade vetorial terá sempre a mesma direção. Como o movimento é uniforme, a velocidade vetorial terá sempre o mesmo módulo e sentido. Podemos então dizer que, nesse caso, a velocidade vetorial é constante.
Movimento retilíneo uniformemente acelerado: Podemos então dizer que, nesse caso, a velocidade vetorial é constante. Como o movimento é acelerado, o módulo da velocidade vetorial aumenta sempre e o sentido se mantém constante
Movimento retilíneo uniformemente acelerado: Como a trajetória é retilínea, a direção da velocidade vetorial se mantém constante. Pelo fato de o movimento ser retardado, o módulo da velocidade vetorial diminui ao longo do tempo. Se a partícula chegar a inverter o sentido do movimento a velocidade vetorial terá o sentido invertido também.
ACELERAÇÃO VETORIAL MÉDIA
Consideremos uma partícula que tem velocidade vetorial v1→ no instante t1 e velocidade vetorial v2→ no instante t2 (com t2 > t1). A aceleração vetorial média da partícula (am→) entre os instantes t1 e t2 é definida por:

CELERAÇÃO VETORIAL INSTANTÂNEA
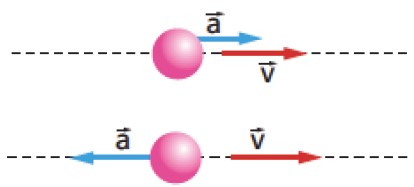
Em uma trajetória retilínea o vetor a→ tem a mesma direção da trajetória e módulo igual ao módulo da aceleração escalar:

Se o movimento for acelerado, a→ terá o mesmo sentido da velocidade vetorial v→ e se o movimento for retardado, a→ terá sentido contrário ao de v→.
COMPOSIÇÃO DE MOVIMENTOS
Movimentos de mesma direção e mesmo sentido
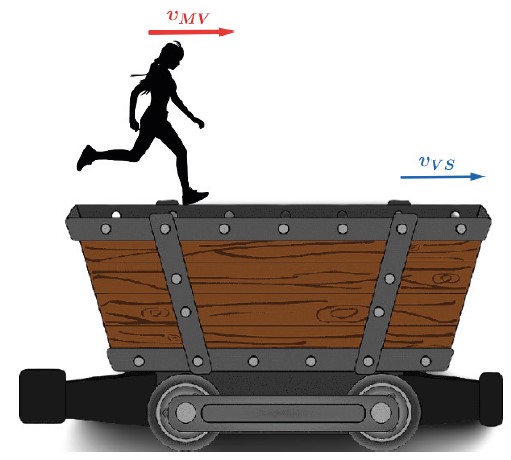
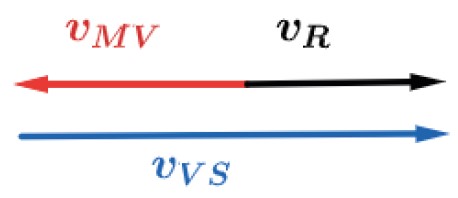
amos supor que uma pessoa, de velocidade vMV→ em relação e um vagão, de velocidade vVS→ em relação ao solo, se movimentam no mesmo sentido.
Nesse caso ambas as velocidades vMV→ e vVS→ tem mesma direção e sentido.
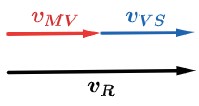
Sendo vR→ a velocidade resultante, ou seja, a velocidade entre a pessoa e o solo, teremos

Movimentos de mesma direção e sentidos opostos
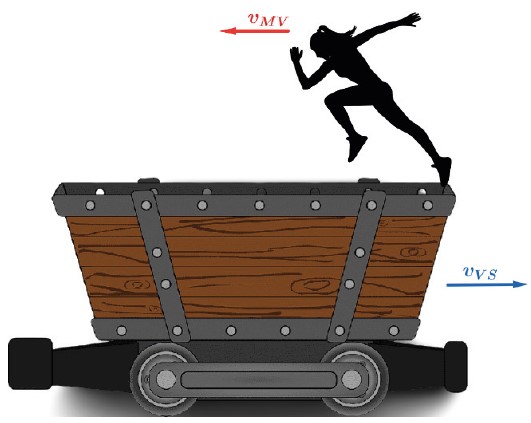
Sendo vR→ a velocidade resultante, ou seja, a velocidade entre a pessoa e o solo, teremos

Exercício Resolvido 2: As águas de um rio retilíneo movimentam-se com velocidade 3,0 m/s em relação às margens. Sobre o rio há duas pontes distanciadas 80 m uma da outra. Um barco, cuja velocidade em relação à água é 5,0 m/s, parte de um ponto situado abaixo de uma das pontes, sobe o rio até a outra ponte e volta para a primeira ponte.
a) Calcule o intervalo de tempo no qual o barco sobe o rio, de uma ponte à outra.
b) Calcule o intervalo de tempo no qual o barco desce o rio, de uma ponte à outra.
c) Qual o intervalo de tempo total de ida e volta? (Despreze o intervalo de tempo gasto pelo barco para virar.)
d) Se o rio estivesse parado em relação às margens, qual seria o intervalo de tempo total de ida e volta?
Resolução:
a) Consideremos as seguintes velocidades:

“Subir o rio” significa “ir contra a correnteza”, isto é, vBA→ e vAM→ têm sentidos opostos.
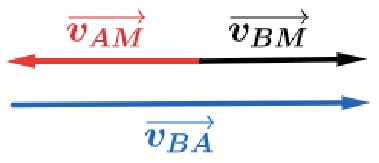
De acordo com o enunciado, temos:

Assim:

Para um referencial fixo nas margens, a distância percorrida pelo barco, para ir de uma ponte à outra, é ∆S = 80 m.
Portanto:

b) “Descer o rio” significa “ir a favor da correnteza”, isto é, vBA→ e vAM→ têm o mesmo sentido.
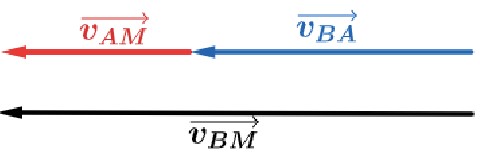
Nesse caso temos:

Portanto:

c) O intervalo de tempo total é obtido adicionando-se o intervalo de tempo de ida ao de volta.
Δt = Δt1 + Δt2 = 40 + 10 = 50 s
d) Se o rio estivesse parado em relação às margens, os intervalos de tempo de ida e volta seriam iguais e teríamos:

Representando por ∆t’ o intervalo de tempo de ida, teríamos:

Portanto, sendo ∆t’’ o intervalo de tempo de ida e volta:

Movimentos de quaisquer direções
O movimento de um ponto material P em relação a um referencial A ou a um referencial B é dado pela soma vetorial dos vetores.
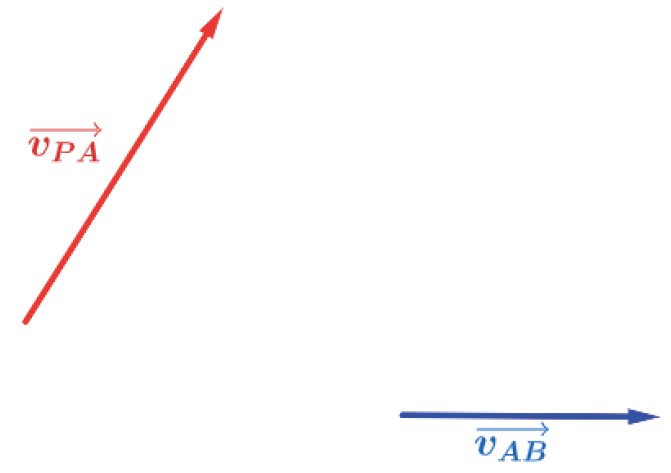
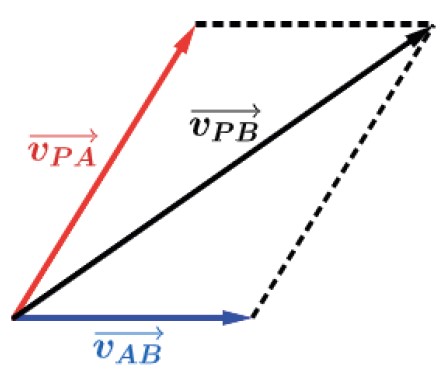
Exercício Resolvido 3: As águas de um rio correm com velocidade v0→ em relação às margens, sendo |v0→| = 6,0 m/s. As margens do rio são paralelas e separadas por uma distância de 24 m. Uma lancha sai de uma das margens em direção à outra, com velocidade v1→ em relação à água, de modo que seu eixo fique perpendicular à correnteza. Sabendo que |v1→ |1 = 8,0 m/s, calcule:
a) o módulo da velocidade da lancha em relação às margens;
b) o intervalo de tempo de travessia;
c) o deslocamento rio abaixo;
d) o deslocamento em relação às margens.
Resolução:
a) Consideremos as seguintes velocidades:

De acordo com o enunciado, temos:

Devemos ter:

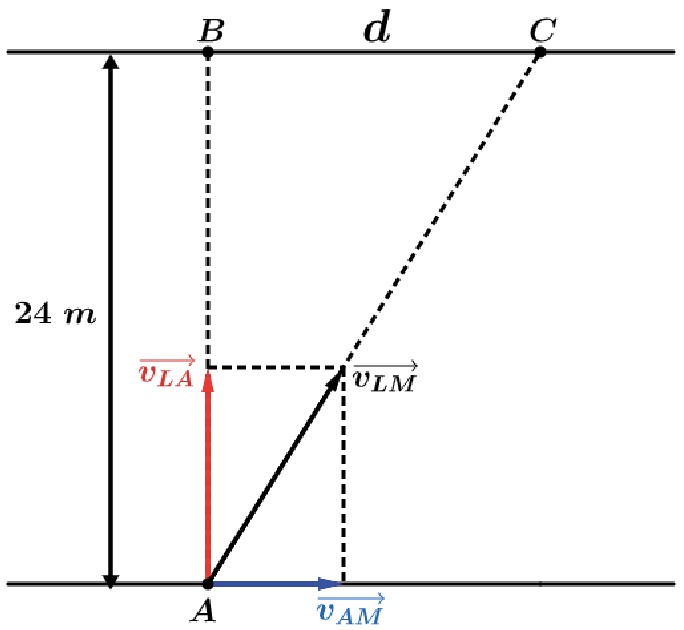
Usando o Teorema de Pitágoras:

Portanto:

b) O movimento da correnteza não interfere no intervalo de tempo da travessia. Podemos fazer o cálculo como se o rio estivesse parado:

c) Ao sair do ponto A em uma das margens (veja a figura), o eixo da lancha aponta para o ponto B da margem oposta. Mas, devido ao movimento da água, a lancha é arrastada lateralmente, indo atingir a margem oposta no ponto C. O deslocamento rio abaixo (d) pode ser calculado, então, usando-se a velocidade da água em relação às margens:

d) Para um observador fixo na margem, a trajetória do barco é o segmento de reta AC¯, cujo comprimento pode ser calculado aplicando-se o Teorema de Pitágoras ao triângulo ABC:
(AC)2 = (AB)2 + (BC)2 = (24)2 + (18)2 ⇒ AC = 30 m
Um outro modo de calcular AC¯ é usar o tempo de travessia e a velocidade VLM→:

É interessante observar que o tempo de travessia pode ser calculado usando-se qualquer uma das três velocidades mencionadas:





