Retas paralelas servem como exemplo de direções iguais.
Semirretas paralelas servem como exemplo de direções e sentidos iguais.
Consideremos um segmento orientado AB, não nulo. Consideremos, em seguida, o conjunto de todos os segmentos orientados que tenham o mesmo módulo, a mesma direção e o mesmo sentido de AB. Esse conjunto é um vetor. Para representar esse vetor, tomamos um segmento orientado qualquer do conjunto. Podemos também indicar um vetor por uma letra com uma flecha “em cima” ou uma letra minúscula com uma flecha em cima.
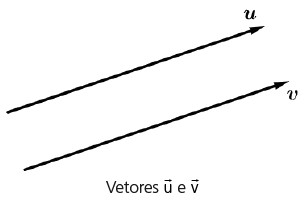
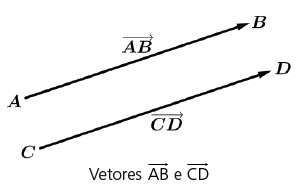
Utilizaremos a representação para os vetores. O módulo de um vetor será representado por |u→|.
Um vetor unitário é aquele que possui módulo igual 1 e assim |u→|=1.
Dois ou mais vetores serão iguais somente se apresentarem mesmo módulo, direção e sentido.

ADIÇÃO E SUBTRAÇÃO DE VETORES
Para fazermos a adição de vetores faremos o seguinte.
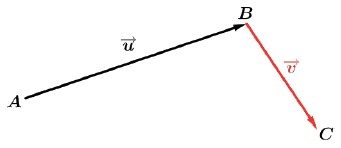
Mantendo-se as direções e os sentidos dos vetores iremos ligar o término do primeiro com o início do segundo.
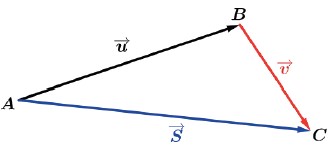
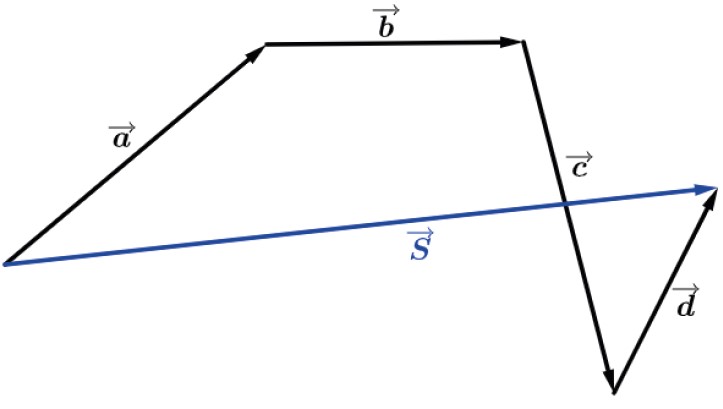
O vetor soma S→ será o vetor que irá ser o “terceiro lado” do triângulo com o sentido do como na figura acima.

Pela desigualdade triangular teremos

Vetores de mesma direção e mesmo sentido
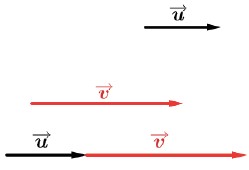

Vetores de mesma direção e sentidos opostos
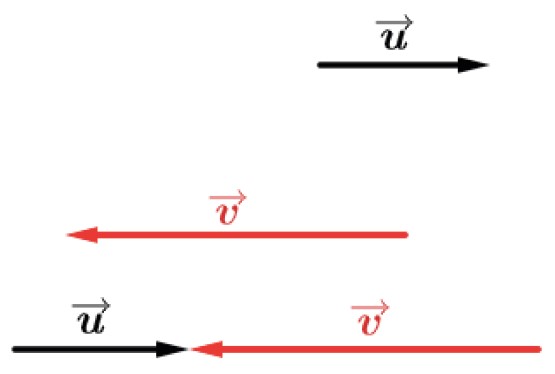


Adição com vetor nulo

Adição de dois ou mais vetores
Regra do paralelogramo
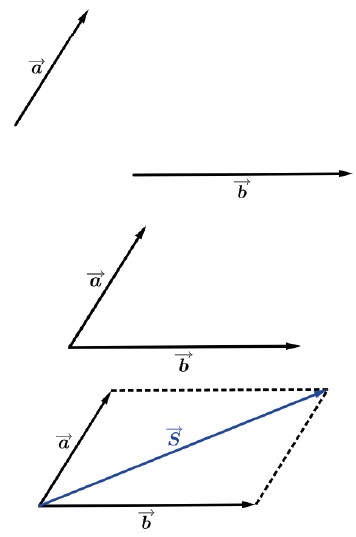
Uma boa opção que podemos utilizar para calcular o módulo do vetor S→ é a Lei dos cossenos na regra do paralelogramo.
Aplicando a Lei dos cossenos no triângulo ABC teremos:

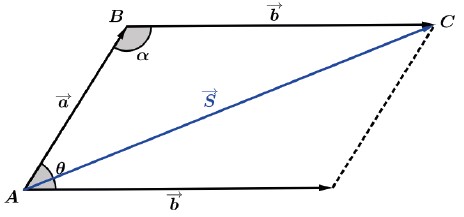
O ângulo θ é o ângulo entre os vetores a→ e b→ mas podemos usar na fórmula o ângulo α.
α = 180° – θ
Sendo assim teremos:
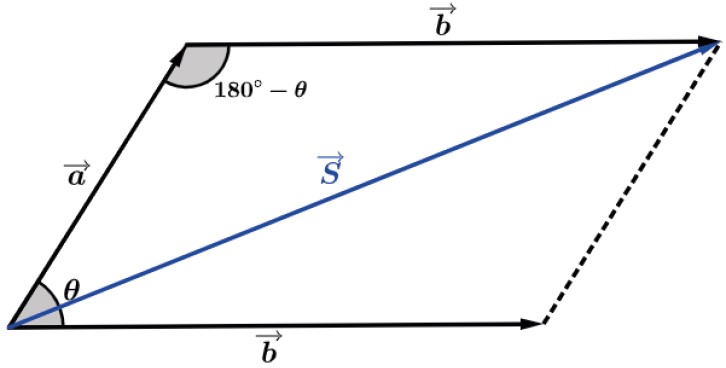

Subtração de vetores

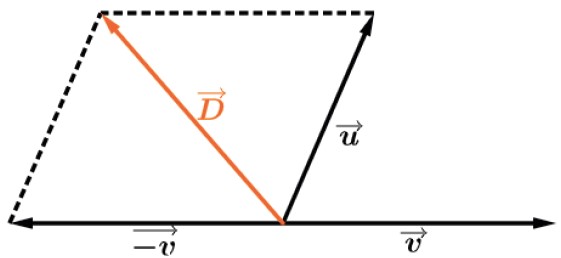
Podemos determinar o vetor D→ também da regra do paralelogramo.
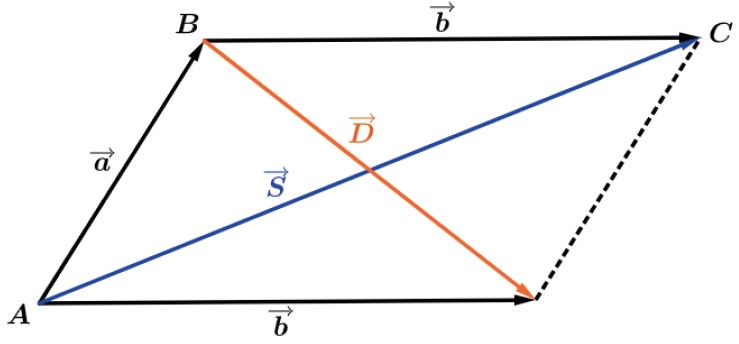
MULTIPLICAÇÃO DE UM VETOR POR UM ESCALAR
Decomposição de um vetor
Será muito comum decompormos um vetor v→ em outros dois vetores perpendiculares entre si.
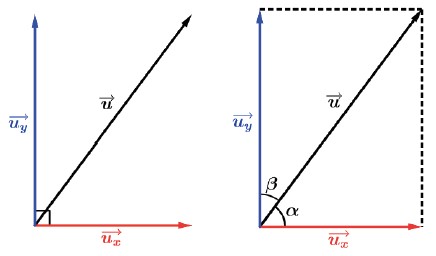
Utilizando as razões trigonométricas no triângulo retângulo teremos

Podemos fazer também

Lembre que se α + β = 90° ⇒ sen α = cos β
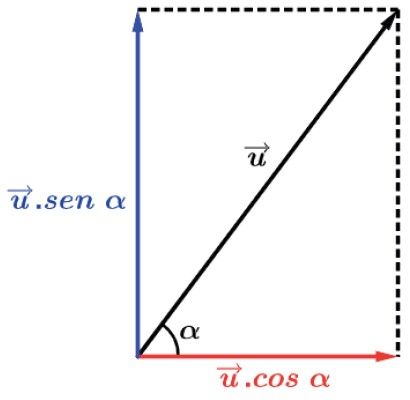
Vamos padronizar a utilização do ângulo formado com a horizontal.
Exemplo: Um vetor a→ de módulo igual a 10 está representado na figura abaixo. Obtenha as componentes de a→ nas direções das retas r e s.
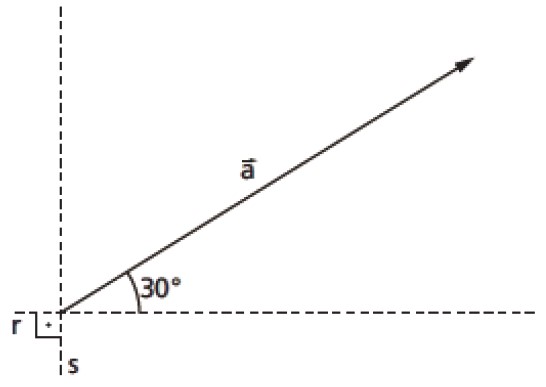
Na figura abaixo estão representadas as componentes pedidas.
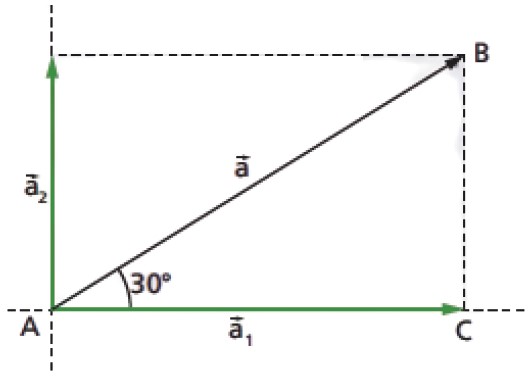
Considerando o triângulo retângulo ABC, temos

Exercício Resolvido 1: (UNIFOR) Um bloco é puxado pela força F→, como ilustra a figura, sendo |F| →=50 unidades = 50 u.
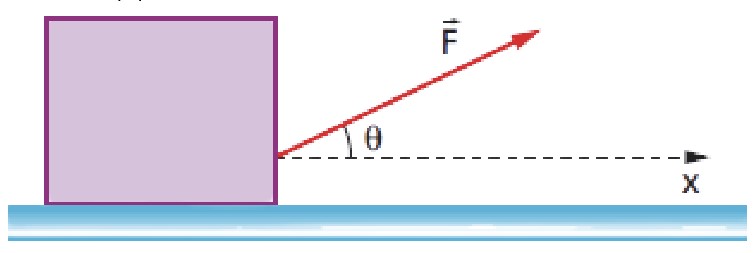
Sabendo que sen θ = 0,80 e cos θ = 0,60, a componente de F→ na direção do eixo x vale:
a) 30 u
b) 40 u
c) 50 u
d) 37,5 u
e) 48 u
Resolução: A
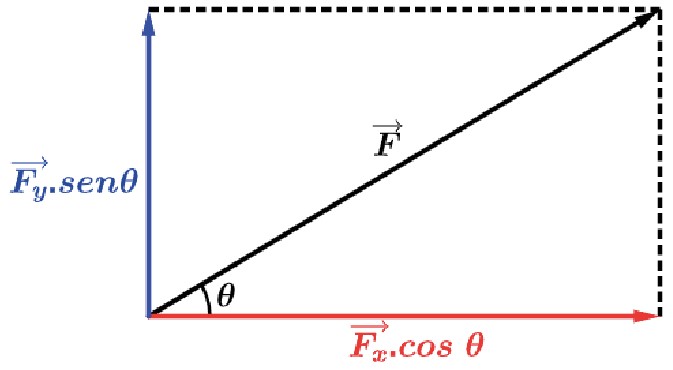
Fx = F . cos θ = 50(0, 6) = 30uFy = F . sen θ = 50(0, 8) = 40u




