ALGARISMOS SIGNIFICATIVOS
Sempre que fazemos uma medição esta não é 100% precisa e isso de dá por diversos fatores que podem incluir desde a expertise de quem está medindo como o limite de precisão do instrumento de medida. Dessa forma sempre há uma incerteza.
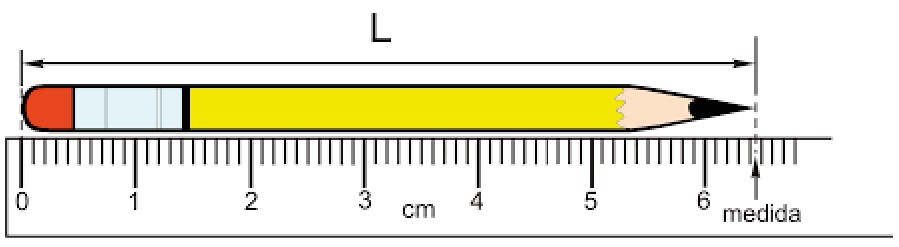
Se tentarmos medir o lápis acima com uma régua graduada em cm vemos que o lápis possui mais de 6 cm e menos de 7 cm. Se formos mais além vamos ver que o lápis possui mais de 6,4 cm e menos de 6,5 cm.
Se dissermos que o lápis possui 6,45 cm estaremos trabalhando com dois algarismos certos, 6 e 4 e com um algarismo duvidoso, o algarismo 5.
Assim algarismos certos são aqueles que podemos ter total certeza a partir da medição executada enquanto que os algarismos duvidosos não.
Na medição do comprimento do lápis temos então 3 algarismos significativos pois teremos o seguinte para algarismos significativos.
Algarismos significativos são os algarismos certos mais o primeiro duvidoso.
Observação: O algarismo 0 quando utilizado somente para determinação da posição da vírgula não é significativo.
Vamos ver um exemplo para o número 0,000610305.

Se quisermos fazer o arredondamento de um número faremos da seguinte forma.
- se o algarismo a ser eliminado for 4 ou menos, o arredondamento é para menos;
- se o algarismo a ser eliminado for 5 ou mais, o arredondamento é para mais.
5,71 ≅ 5,7 e assim 5,7 ≅ 6,0
4,38 ≅ 4,4 e assim 4,4 ≅ 4,0
ANÁLISE DIMENSIONAL
Com exceção das grandezas suplementares, qualquer outra grandeza tem suas unidades expressas em função das unidades básicas; por isso, essas unidades são chamadas unidades derivadas.
E ainda temos:
- Unidade de área = (unidade de comprimento)²
- Unidade de volume = (unidade de comprimento)³
Vamos utilizar a seguinte simbologia: comprimento (L), tempo (T) e massa (M).
Quando temos uma grandeza mecânica G qualquer, é costume apresentar sua equação dimensional usando-se sempre as três dimensões básicas: primeiramente L, depois M e em seguida T. Assim, em geral, a equação da grandeza G terá a forma:

Dizemos que uma grandeza adimensional quando ela não possui unidade. Vamos pensar na unidade da densidade. A densidade é a razão entre a massa e o volume.

Assim teremos como unidade de densidade o seguinte

Se definirmos a densidade relativa entre dois corpos de densidades d1 e d2 como

Assim a unidade da densidade relativa será adimensional.

Assim [dr] = L0M0T0




