CILINDRO
CILINDRO CIRCULAR
Dado um círculo de centro O e raio R situado num plano αα, e um segmento de reta PQ, não nulo, não paralelo e não contido em α, chama-se cilindro circular ou cilindro a reunião dos segmentos congruentes e paralelos a PQ, que tem uma extremidade no círculo e situados num mesmo semi-espaço dos determinados por α.
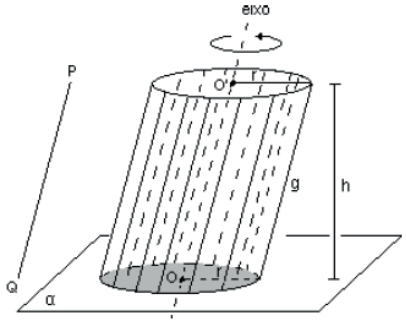
ELEMENTOS, DENOMINAÇÃO E CLASSIFICAÇÃO
- Os círculos congruentes situados em planos paralelos são as bases do cilindro;
- Geratriz g e todo segmento com uma extremidade
- em um ponto da circunferência de centro O e raio r e outra no ponto correspondente da circunferência de centro O’ e raio r;
- A altura h de um cilindro e a distância entre os planos das bases;
- Se as geratrizes são obliquas aos planos das bases, o cilindro e dito cilindro circular oblíquo (figura do exemplo), mas se são perpendiculares aos planos das bases, temos um cilindro circular reto ou de revolução.
ÁREAS
ÁREA DA BASE – SB
E a área do círculo da base do cilindro.
SB = πr2
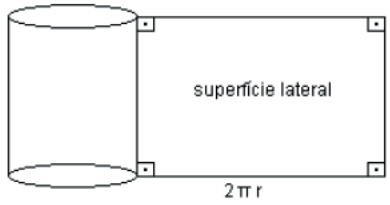
ÁREA LATERAL – SL
Superfície lateral e a reunião das geratrizes. A área dessa superfície e chamada área lateral SL é dada por:
SL = 2πrh
ÁREA TOTAL – ST
Superfície total e a reunião da superfície lateral com os círculos das bases. A área dessa superfície e denominada área total e é dada por:
ST = SL + 2SB
ST = 2πr(h + r)
VOLUME
O volume de um cilindro e o produto da área da base pela medida da altura.
V = πr2h
CILINDRO EQUILÁTERO
O cilindro que possui as seções meridianas quadradas é chamado de cilindro equilátero. No cilindro equilátero a altura é igual ao diâmetro da base.
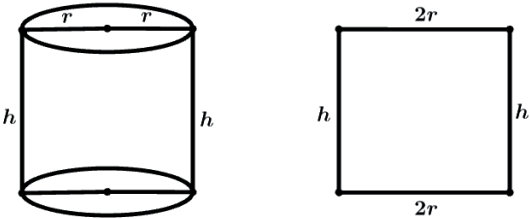
h = 2r




