Cilindro

CILINDRO CIRCULAR

Considere dois planos paralelos, α e β, seja R um círculo no plano α, seja s uma reta secante aos dois planos que não intersecta R, o conjunto de todos os segmentos de retas paralelos a s que contém um ponto de R e um ponto no plano paralelo β formam um cilindro.

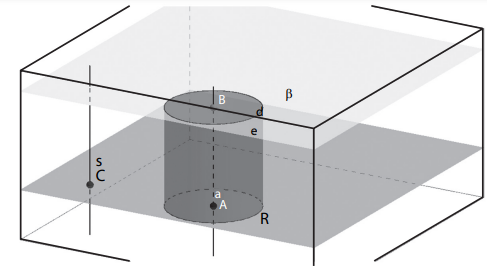
Todo cilindro possui três superfícies, as duas bases e a superfície lateral. O eixo do cilindro é a reta que passa pelos centros das suas bases, na figura acima a reta que passa pelos pontos A e B. Se o eixo for perpendicular às bases o cilindro será circular reto, caso contrário, será um cilindro oblíquo.

DEFINIÇÕES

Superfície cilíndrica de revolução é a superfície gerada pela rotação de uma reta g (geratriz) ao redor de uma reta fixa paralela OO’ (eixo). A distância constante entre g e OO’ é o raio. A circunferência descrita por qualquer ponto de D é um paralelo. Qualquer plano que passe por OO’ é chamado plano meridiano.

Seção reta é a seção da superfície cilíndrica por qualquer plano perpendicular às geratrizes.

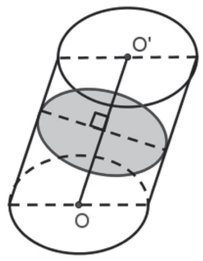
Um cilindro é reto ou oblíquo conforme suas bases sejam seções retas ou oblíquas da superfície cilíndrica.

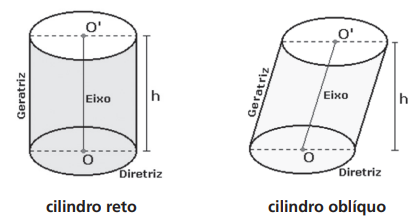
Observação: No cilindro circular reto a geratriz é igual à altura. No cilindro circular oblíquo a geratriz é maior que a altura.

VOLUME

O volume do cilindro é calculado pelo produto da área da sua base pela sua altura.

V = A_B ⋅ h = πr²h

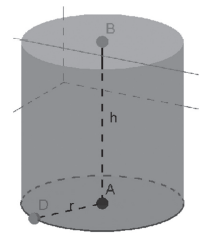
ÁREA LATERAL E ÁREA TOTAL DO CILINDRO CIRCULAR RETO

Planificando o cilindro circular reto obtemos:

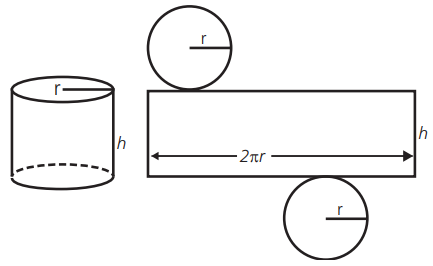
Portanto sua área lateral do cilindro circular reto é igual a área do retângulo de dimensões 2 · π · r e h.

O comprimento do retângulo 2 · π · r é igual ao perímetro da circunferência da base do cilindro.

Portanto a área lateral é dada por A_I = 2 ⋅ π ⋅ r ⋅ h.

E a sua área total é dada pela soma da área lateral com as áreas das duas bases.

Área total = A_t = A_I + 2A_b – 2 · π · r · h + 2 · π · r² = 2 · π · r · (r + h)

SEÇÃO MERIDIANA DE UM CILINDRO CIRCULAR (QUADRILÁTERO ABCD)

É a interseção do cilindro com um plano que contém a reta que liga os centros das bases (OO’).

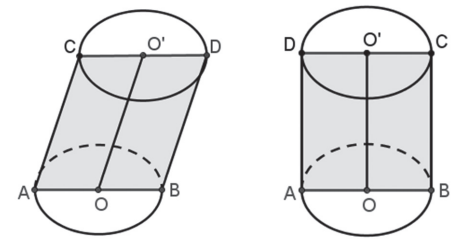
No cilindro oblíquo a seção meridiana é um paralelogramo e no cilindro reto é um retângulo.

CILINDRO EQUILÁTERO

O cilindro que possui as seções meridianas quadradas é chamado de cilindro equilátero. No cilindro equilátero a altura é igual ao diâmetro da base.

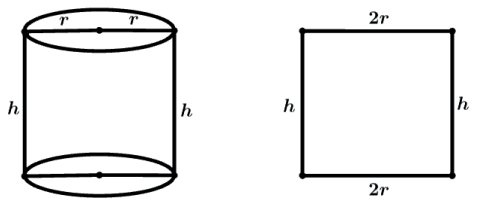
h=2r

Como consequências imediatas, temos para o cilindro equilátero

Área lateral – S_L

S_L = 2πrh = 2πr ⋅ 2r = 4πr²

Área total – S_T

S_T = 2S_B + S_L = 2πr² + 4πr² = 6πr²

Volume – V

V = πr²h = πr² . 2r = 2πr³