Assim como a Terra tem um campo gravitacional, uma carga Q também possui um campo que pode influenciar as cargas de prova q nele colocados. E, usando esta analogia, podemos encontrar:
P = m · g
Desta forma, assim como para a intensidade do campo gravitacional, a intensidade do campo elétrico (E) é definida como o quociente entre as forças de interação das cargas geradoras do campo (Q) e de prova (q) e a própria carga de prova (q), ou seja:

O campo elétrico determina o local onde as forças elétricas estão concentradas por meio da ação das cargas elétricas puntiformes (corpo eletrizado cujas dimensões e massa são desprezíveis se comparadas às distâncias que o afastam de outros corpos eletrizados). O sentido do campo elétrico depende exclusivamente do sinal da carga elétrica, por isso, importante notar que o campo elétrico existe por meio de sua interação com uma carga de prova, de modo que as que apresentam mesmo sinal, sofrerão uma repulsão, e as cargas, de sinais contrários, sofrerão uma atração.
Desse modo, quando o campo elétrico é criado numa carga positiva, ele terá um sentido de afastamento ou repulsão, por sua vez, quando é gerado numa carga negativa, ele terá um sentido de aproximação ou de atração.
VETOR CAMPO ELÉTRICO
Voltando à analogia com o campo gravitacional da Terra, o campo elétrico é definido como um vetor com mesma direção do vetor da força de interação entre a carga geradora Q e a carga de prova q e com mesmo sentido se q > 0 e sentido oposto se q < 0. Ou seja:

A unidade adotada pelo SI para o campo elétrico é o N/C (Newton por coulomb).

Partindo de que:

e que

Após alguns cálculos, chegamos a:

Interpretando esta unidade, podemos concluir que o campo elétrico descreve o valor da força elétrica que atua por unidade de carga para as cargas colocadas no seu espaço de atuação.
CAMPO ELÉTRICO GERADO POR MAIS DO QUE UMA PARTÍCULA ELETRIZADA
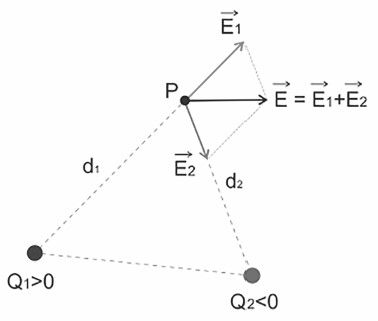
Quando duas ou mais cargas estão próximas o suficiente para que os campos gerados por cada uma se interfiram, é possível determinar um campo elétrico resultante em um ponto desta região.
Para isto, analisa-se isoladamente a influência de cada um dos campos gerados sobre um determinado ponto.
O vetor do campo elétrico resultante será dado pela soma dos vetores no ponto P. Como ilustra o exemplo a seguir:
LINHAS DE FORÇA
Estas linhas podem ser consideradas a representação geométrica convencionada para indicar a presença de campos elétricos, sendo representadas por linhas que tangenciam os vetores campo elétrico resultante em cada ponto, logo, jamais se cruzam. Por convenção, as linhas de força têm a mesma orientação do vetor campo elétrico, de modo que, para campos gerados por cargas positivas, as linhas de força são divergentes (sentido de afastamento) e campos gerados por cargas elétricas negativas são representados por linhas de força convergentes (sentido de aproximação).
Quando se trabalha com cargas geradoras sem dimensões, as linhas de força são representadas radialmente, de modo que:
DENSIDADE SUPERFICIAL DE CARGAS
Um corpo em equilíbrio eletrostático, ou seja, quando todos possíveis responsáveis por sua eletrização acomodam-se em sua superfície, pode ser caracterizado por sua densidade superficial média de cargas σm. A densidade de carga linear, superficial ou volumétrica é uma quantidade de carga elétrica em uma linha, superfície ou volume, respectivamente.

Sendo sua unidade adotada no SI o C/m².
Observe que, para cargas negativas, a densidade superficial média de cargas também é negativa, já que a área sempre é positiva.
Utiliza-se o termo médio já que dificilmente as cargas elétricas se distribuem uniformemente por toda a superfície de um corpo, de modo que é possível constatar que o módulo desta densidade é inversamente proporcional ao seu raio de curvatura, ou seja, em objetos pontiagudos eletrizados há maior concentração de carga em sua extremidade (ponta).
CAMPO ELÉTRICO UNIFORME
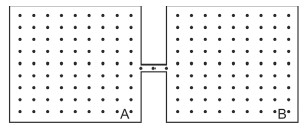
Um campo elétrico é uniforme numa determinada região do espaço se tiver as mesmas características em todos os seus pontos. Nesse caso, as linhas de campo elétrico são paralelas.
Um campo elétrico uniforme pode ser criado por duas placas metálicas paralelas, entre as quais se estabelece uma diferença de potencial constante. Uma carga elétrica q colocada em qualquer ponto do campo uniforme experimenta uma força elétrica com a mesma intensidade e o mesmo sentido.
A LEI DE GAUSS
A lei de Gauss é a lei que estabelece a relação entre o fluxo do campo elétrico através de uma superfície fechada com a carga elétrica que existe dentro do volume limitado por esta superfície. Isto é, o valor do campo é o mesmo para qualquer ponto sobre uma esfera. Mais do que isso, o campo deve ser normal a esta esfera.
Portanto, a melhor Gaussiana para calcular o campo a uma distância r de uma carga puntiforme é uma esfera de raio r.
Em qualquer ponto sobre a Gaussiana, o produto escalar será simplesmente EdS. Então, tendo em conta que E é constante, teremos:

A integral fechada sobre a superfície corresponde à área da esfera, 4 π . r2. Portanto, o campo de uma carga puntiforme, q, a uma distância r, é dado por





