FATORIAL
Definimos fatorial de um número natural n, tradicionalmente denotado por n!, ao número definido indutivamente por: 0! = 1 e n! = n(n–1)!
Temos que n!, logo tem-se que 5! = 5 · 4 · 3 · 2 · 1 = 120; 3! = 3 · 2 · 1 = 6; etc…
COEFICIENTES BINOMIAIS
DEFINIÇÃO
Dados os naturais n e k, sendo n ≥ k chama-se coeficiente binomial n sobre k e se indica:

Da definição que para 1 ≤ k ≤ n tem-se:

Exemplo: calcule n, sabendo-se que (n+1)!/n! = 7.
Solução: temos que (n + 1)! = (n + 1) · n · (n – 1) ·…· 3 · 2 · 1 = (n + 1) · n!

TRIÂNGULO DE PASCAL
O triângulo de Pascal é um triângulo aritmético formado por números que têm muitas relações entre si. Algumas dessas relações foram descobertas por Pascal.
Onde Ckn representa combinação de n escolhe k, n é o número da linha e k representa o número da coluna.
Os quadros abaixo representa o triângulo de Pascal:

RELAÇÃO DE STIFEL
Trata-se de uma propriedade que permite construir o Triângulo de Pascal dada pela seguinte fórmula:

Somando 2 elementos consecutivos de uma mesma linha obtemos o elemento localizado abaixo da segunda parcela.
Prova: considere o número de comissões de p + 1 pessoas que podemos formar a partir de um grupo de n+1 pessoas, sabendo que uma destas n + 1 pessoas é Pedro.
O total dessas comissões é igual a Cp+1n+1 , por outro lado podemos contar este total separando em dois casos; primeiro caso comissões que Pedro participa que são Cpn e o segundo caso, as comissões na qual Pedro não participa que são Cp-1n .
TEOREMA DAS LINHAS
A soma dos termos da linha n é igual a 2n.

Prova: seja o conjunto A={1,2,3,…,n} o total de subconjuntos é igual a

Por outro lado, para formar um subconjunto de A, cada elemento de A tem duas opções, participar ou não do subconjunto.
Concluímos que o total de subconjuntos é igual a 2n.
TEOREMA DAS COLUNAS
A soma dos elementos de uma coluna do triângulo, começando no primeiro termo da coluna, é igual ao elemento que está na linha e na coluna posteriores ao último elemento da soma.

Prova: considere o conjunto A={1, 2,…, p,…, n + p, n + p + 1} com p < n, o total de subconjuntos de p + 1 elementos de A é igual a Cp+1n+p+1.
Por outro lado cada um destes subconjuntos tem um elemento que é o máximo (maior elemento do conjunto).
Primeiro caso: p + 1 é o máximo, os outros p elementos são escolhidos a partir de {1, 2,…, p}.
Total de subconjuntos = Cpp.
Segundo caso: p + 2 é o máximo; agora devemos escolher os outros p elementos de elementos {1, 2,…, p + 1}.
Total subconjuntos: = Cpp+1.
Caso N: n+p+1 é o máximo. Agora devemos escolher os outros p elementos a partir do conjunto {1,2,…,n+p}.
Total de subconjuntos = Cpn+p.
Igualando as duas formas, o teorema está provado.
OUTRAS PROPRIEDADES

BINÔMIO DE NEWTON
Consideremos a igualdade: (x + a)n = (x + a)( x+ a) … (x + a)(n fatores )(1)
Para se formar um termo do produto (x + a)(x + a) … (x + a) devemos escolher uma das duas parcelas em cada um dos n fatores x + a e efetuar o produto das mesmas.
Por exemplo, se escolhermos p letras a em p dos n binômios, e n–p letras x dos n–p binômios restantes, então um termo genérico do desenvolvimento de (x + a)n é da forma:

O número de termo da forma (2) é, então é igual ao número de modos de escolhermos p letras a em p dos n binômios x + a, isto é Cpn.
Portanto, reduzindo todos os termos da forma apxn-p, encontramos um único termo, Cpnapxn-p.
Finalmente, fazendo p variar de 0 até n, encontramos todos os termos do desenvolvimento de (x + a)n.

Expandindo o somatório acima, temos:

TERMO GERAL DO DESENVOLVIMENTO DE (x + a)n
Todos os termos do desenvolvimento de (x + a)n são obtidos de
Por este motivo, Cpnapxn-p é chamado de termo geral.
Chamando o 1º, 2º, 3º, …termos do desenvolvimento de (x + a)n respectivamente por T1,T2,T3, …, podemos observar que:

Isto é, a ordem de cada termo é igual à taxa da combinação correspondente mais 1. Como a taxa da combinação do termo geral é p, segue-se que este termo é de ordem p+1. Isto é, Tp+1 = Cpnapxn-p
Exemplo: na expansão de (x + 2)4
Pela linha do triângulo de Pascal temos os números binomiais
1 4 6 4 1
Mas teremos também a regra dos expoentes aplicada aos termos do binômio a ser expandido, x e 2.

Como nossa expansão é (x + 2)4 teremos todos os sinais positivos, assim:
(x+2)4 = x4 + 8x3 + 24x2 + 32x + 16
Se tivéssemos a expansão de (x + 2)4 iremos ter os sinais alternantes
(x – 2)4 = x4 – 8x3 + 24x2 – 32x + 16
Exemplo: encontrar o coeficiente de x4 na expansão de (2/x – x4)6.
Esse talvez seja o tipo de problema que mais iremos encontrar. Devemos primeiro utilizar nossos conhecimentos de propriedades de potência e arrumar nossos termos a e b do binômio.

Para utilizarmos na nossa fórmula do termo geral Tp+1 = (np) · xn-p · ap podemos ainda pensar o seguinte:
(2x-1 – x4)6 = (2x-1 + (-x4))6 = (2x-1 + (-1 · x4))6
Sendo assim temos a = 2x-1, b = (-1) · (x4) e n = 6.
Pela nossa fórmula:

Nosso termo geral possui como termo algébrico x5p-6 de onde deveremos igualar 5 p – 6 a 4, para termos o que a questão pediu, o termo x4.
5p – 6 = 4 → 5p = 10 → p = 2
Sendo p = 2

Então o termo que possui x4 é o 3º Termo do desenvolvimento (p + 1) e

Observação:
Toda vez que nos for pedida a soma dos coeficientes de um polinômio (uma expansão binomial não deixa de resultar em um polinômio) basta fazermos x=1.
Sendo assim, qual a soma dos coeficientes da expansão (x + 1)10? Responder essa pergunta é fácil, pois temos a tendência de achar que só podemos respondê-la depois de totalmente expandido o binômio, o que não é verdade.
(x+1)10 = x10 + 10x9 + 45x8 + 120x7 + 210x6 + 252x5 + 210x4 + 120x3 + 45x2 + 10x + 1
Podemos tanto fazer x=1 do lado direito da igualdade (o que é bem mais trabalhoso porque muitas vezes expandir não será fácil) como fazer x=1 no lado esquerdo da igualdade.
Então a soma de todos os coeficientes da expansão de (x + 1)10 = (1 + 1)10 = (2)10 = 1024.
Agora confira você se 1024 não é realmente a resposta só que fazendo x=1 do lado direito da igualdade.
Estando preparado para não cair mais em pegadinhas diga pra mim qual a soma dos coeficientes da expansão de (3x – 1)7 . 3
POLINÔMIO DE LEIBNIZ
Existe uma generalização do binômio de Newton onde com ele podemos fazer uma expansão de qualquer quantidade de termos, chama-se Polinômio de Leibniz.

Estendendo-se o somatório a todos os valores inteiros não negativos de α1 , α2 ,…, αp tais que α1 + α2 + … + αp = n.
Vamos ver um exemplo prático com um exemplo? Claro que com 3 termos! Vamos desenvolver (x2 - x + 2)6

Vamos escolher agora um expoente e ver qual será o coeficiente que irá acompanhar este termo. Por exemplo, vamos escolher o expoente 3.

Vamos utilizar uma tabela auxiliar
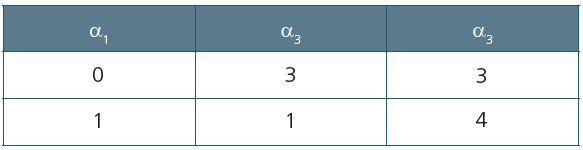
Para α1 = 0, α2 = 3 e α3 = 3

Nosso total é -160x3 – 480x3 = -640x3.




