BARICENTRO DE UM TRIÂNGULO
Baricentro é o ponto de encontro de todas as medianas de um triângulo. Lembre-se que o baricentro sempre divide a mediana na razão de 2 : 1. A distância do vértice ao baricentro (G) é o dobro da distância do baricentro ao lado.
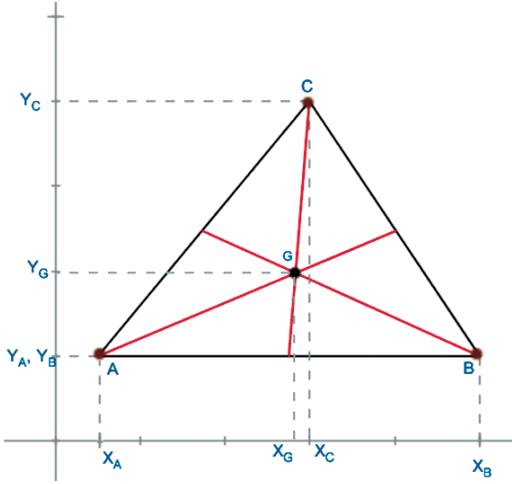

Assim, o baricentro do triângulo ABC será:

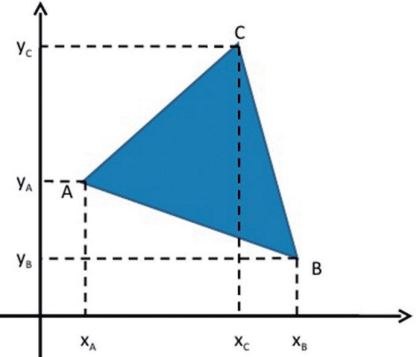
ÁREA DO TRIÂNGULO

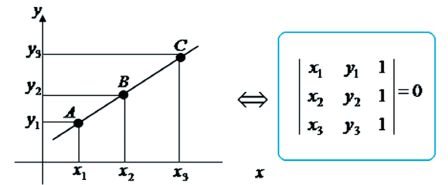
CONDIÇÃO DE ALINHAMENTO DE TRÊS PONTOS
Podemos pensar que se temos 3 pontos alinhados esses pontos não podem formar um triângulo, logo se não podem formar um triângulo não há área (s = 0). Dessa forma devemos igualar o determinante a0.
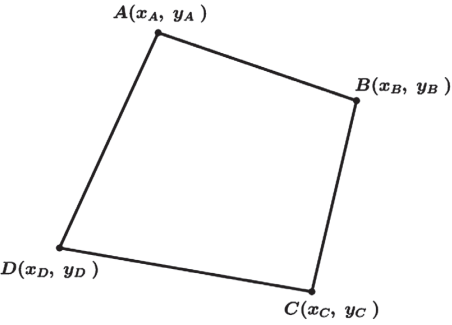
ÁREA DE UM POLÍGONO QUALQUER
Podemos encontrar a área do triângulo a partir das coordenadas dos seus 3 vértices através do seguinte algoritmo.

Perceba que a última linha será a coordenada do mesmo ponto utilizado na primeira linha. Assim para calcularmos a área de um triângulo teremos 4 linhas, um quadrilátero 5 linhas, …, e assim para qualquer quantidade de vértices do polígono.

O processo se dá de forma semelhante ao cálculo do determinante

Exemplo: Calcular a área do quadrilátero A(2, –1), B(4, 5), C(3, –3) e (–4, 0).





