Consideremos um bloco de massa m, abandonado em repouso sobre uma superfície S, plana e sem atrito, a qual forma um ângulo a com um plano horizontal.
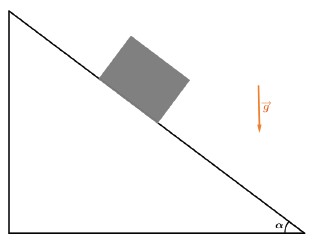
As forças que atuam no bloco são o seu peso P→ e a força normal FN→ exercida pela superfície S sobre o bloco.
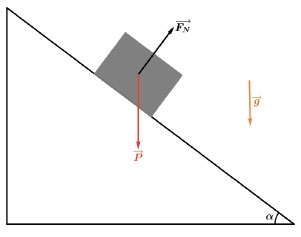
demos decompor o peso em duas componentes: uma componente Px→, paralela à superfície S, e outra componente Py→, perpendicular a S.
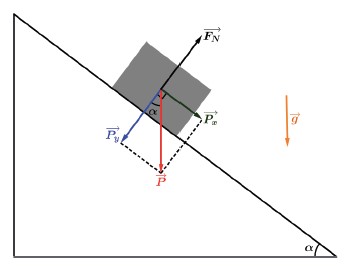
Fazendo a decomposição, teremos:

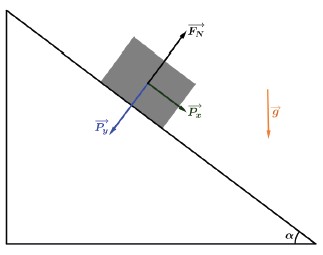
A força Px é a responsável por fazer o bloco descer e dessa forma:
Px = m · a
Temos também
Px = m · a ⇒ P · sen θ = m · a ⇒ m · g · sen θ = m · a ⇒ a = g · sen θ
É importante observar na igualdade a = g · sen θ que a aceleração não depende da massa do bloco. No temos também que a equação a = g · sen θ vale apenas quando as únicas forças atuantes no bloco são o peso e a força normal. Se houver outras forças, a aceleração poderá ser diferente.
Observação: A inclinação de um plano pode ser dada em percentual. Sendo assim, um plano inclinado de 80% significa que tg α = 80% = 0,80. Assim se um plano inclinado possui uma inclinação de k % significa que tg α = k/100.
Exemplo: Uma partícula é abandonada sobre um plano inclinado de 50%. Desprezando o atrito e adotando g = 10 m/s², calcule o módulo da aceleração adquirida pela partícula.
Resolução:

sendo assim:


Vimos que a = g · sen θ, então:





