Há situações ideais em que as forças de atrito são desprezadas.
Podemos dizer que as forças de atrito são tangentes as superfícies em contato e tem sentido oposto ao de movimento ou a tendência de movimento.
Existem casos em que a força de atrito se dá no mesmo sentido do movimento.

rimeiramente só conseguimos andar por existir o atrito pois senão nossos pés escorregaríamos na superfície não conseguiríamos andar. Como vimos no módulo anterior, o pé de uma pessoa caminhando aplica uma força sobre a superfície e essa por sua vez aplica uma força de mesma intensidade e direção, mas de sentido contrário. Esse par de ação e reação formado são forças de atrito.
Há dois tipos de forças de atrito, quando há movimento relativo entre as superfícies em contato, chamada de força de atrito dinâmico ou força de atrito cinética e quando não há movimento relativo entre as superfícies em contato, a força de atrito é chamada de força de atrito estático.
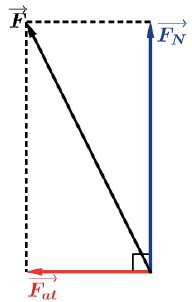
Exemplo: Um bloco de massa 2,0 kg é lançado com velocidade inicial v0 = 10 m/s sobre uma superfície horizontal S. Devido ao atrito, o bloco para após percorrer uma distância de 10 metros. Despreze a resistência do ar e suponha g = 10 m/s². Supondo que a força de atrito tenha sido constante durante o deslizamento, pede-se:
a) o módulo da força de atrito durante o movimento;
b) o módulo da força total exercida pela superfície sobre o bloco durante o movimento.
Resolução:
a) Utilizando a equação de Torricelli teremos:


b) Teremos a força normal FN→ e a força de atrito Fat→ aturando no corpo.
FN = mg = 2 . 10 = 20 N

FORÇA DE ATRITOR DINÂMICO
A força de atrito dinâmico tem seu módulo dado por
Fat = μd · FN
Onde FN é a força normal que um corpo exerce no outro e μd é o coeficiente de atrito de dinâmico ou cinético. O coeficiente de atrito dinâmico depende única e exclusivamente do material que cada corpo é confeccionado bem como do estado de polimento e lubrificação das superfícies de contato. Como μd = Fat/FN temos que μμd é adimensional.
FORÇA DE ATRITO ESTÁTICO
Quando não há movimento relativo entre as superfícies de contato de dois corpos, a força de atrito, desde que exista, é chamada força de atrito estático. O módulo da força de atrito estático é variável.
Imagine o sofá da sua casa, ele está lá parado, em repouso, então não há forças atuando sobre ele além do peso e da normal. Você precisa movimentar o sofá para limpar debaixo dele e para isso começa a aplicar uma força gradativa, o sofá permanece parado pois conforme você começa a aplicar uma força sobre o sofá também começa a surgir uma força de atrito estático. Conforme você vai aumentando a força a força de atrito também vai aumentando, pois o sofá não se mexe e a força de atrito estático é a responsável por isso. Chega um momento que sua força vence a força de atrito estático pois esta possui um valor máximo. Quando a força de atrito estático atinge o seu valor máximo, mas o bloco continua em repouso, dizemos que o bloco está na iminência de movimento.
Fatmax = μe · FN
Temos que μe ≥ μd.
Já parou para pensar que muitas vezes é mais difícil empurrar ou puxar um objeto para tirá-lo da inércia do que, depois de em movimento, mantê-lo?
Observação: Ângulo de atrito é o ângulo q, de um plano inclinado, onde a inclinação q é a inclinação mínima necessária para que um corpo esteja na iminência de deslizamento no plano inclinado.

Exemplo: Consideremos um corpo de massa m = 12 kg inicialmente em repouso sobre uma mesa horizontal. Sabe-se que g = 10 m/s² e que os coeficientes de atrito estático e dinâmico entre o corpo e a mesa são respectivamente μe = 0,70 e μd = 0,40. Aplicamos ao corpo uma força horizontal F→.
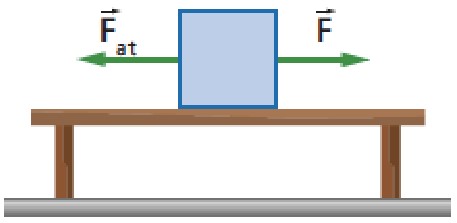
Calcule o módulo da força de atrito atuante no corpo e o módulo da aceleração do corpo após a aplicação de F→, nos seguintes casos:
a) F = 60 N
b) F = 84 N
c) F = 90 N
Resolução:
Temos que a força normal FN→ tem módulo igual ao da força peso.
FN = m · g = 12 · 10 = 120 N
Teremos uma força de atrito estática máxima
Fatmax = μe · FN = 0,7 · 120 = 84 N
a) Para uma força de 60N a força de atrito será menor que a força de atrito máxima e dessa forma o bloco permanecerá em repouso e a Fat = 60 N.
b) Para uma força de 84 N o bloco estará na iminência do movimento, ainda em repouso e Fat = 84 N.
c) Para uma força de 90 N já estará em movimento pois a força aplicada é maior que a força de atrito estático máxima. Sendo assim
Fat = μdFN = 0,4 · 120 = 48 N
Teremos
F – Fat = m · a ⇒ 90 – 48 = 12 · a ⇒ 12a = 42 ⇒ 3,50 m/s²
Observação: Em um plano inclinado com atrito, o movimento do bloco se dará por
Px – Fat = m · a
FORÇA ELÁSTICA
É a força que surge em uma mola quando a deslocamos da sua posição natural.
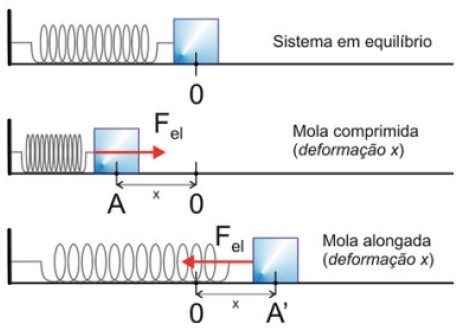
Ela é proporcional à sua deformação e possui sentido contrário ao deslocamento, sendo uma força restauradora, que pode ser calculada pela expressão:
Fel = k · x
Em que:
- k é a constante elástica da mola, cuja unidade é o N/m.
- x é a deformação, ou seja, a diferença entre comprimento final e seu comprimento natural.
Observação: Existem outras forças como resistência do ar e tração, mas elas só serão vistas na forma de exercício.




