Em muitas situações será conveniente decompor uma força em direções perpendiculares. Podemos decompor uma força F→ em duas forças perpendiculares:

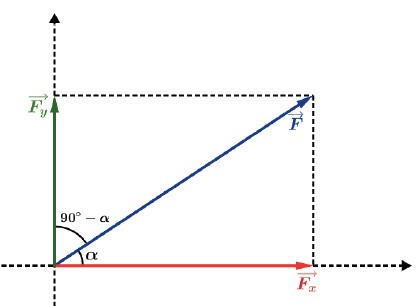
Da trigonometria teremos:

Da trigonometria temos que sen (90° – α) = cos α e cos (90° – α) = sen α o que nos mostra que utilizando as relações para o ângulo (90° – α) encontraríamos os mesmos valores.
Observação: Que direções utilizar em uma decomposição de forças?
Se a partícula tem aceleração a→ não nula o mais conveniente, em geral, é considerarmos direções perpendiculares tais que uma delas seja coincidente com a direção da aceleração a→.
Exemplo: Um bloco de massa m = 15 kg está inicialmente em repouso sobre um plano horizontal sem atrito, num local onde g = 10 m/s². A partir de determinado instante aplica-se ao bloco uma força constante F→, como mostra a figura:

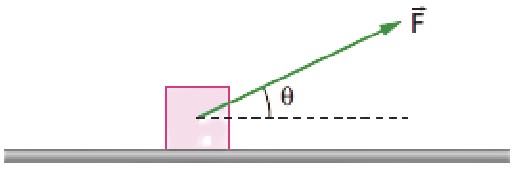
A partir do instante em que F é aplicada, calcule:
a) o módulo da força normal exercida pelo plano horizontal sobre o bloco;
b) o módulo da aceleração adquirida pelo bloco.
Resolução:
a) Suponhamos que o movimento do bloco seja retilíneo e horizontal, isto é, que o bloco não perca o contato com o plano horizontal e assim sua aceleração a tenha direção horizontal. Mais adiante veremos se a hipótese está correta. As forças que atuam no bloco são o peso P→, a força normal FN→ e a força F→.
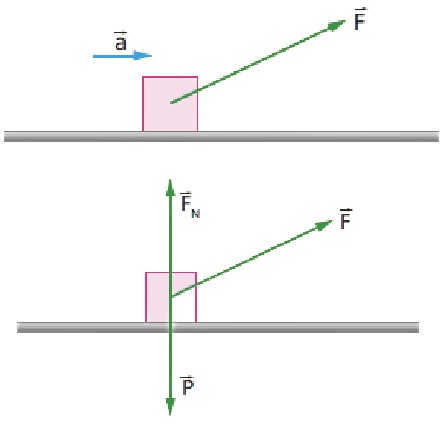
Temos:
P=m · g = 15 · 10 ⇒ P = 150 N
Como estamos supondo que a aceleração a→ tem direção horizontal, vamos decompor a força F→ em duas direções perpendiculares tais que uma delas seja horizontal. Temos, então:

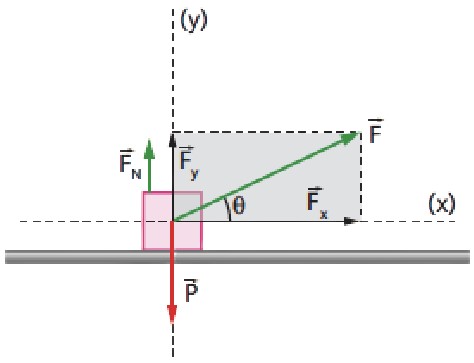
O esquema real de forças, que é o da figura abaixo.
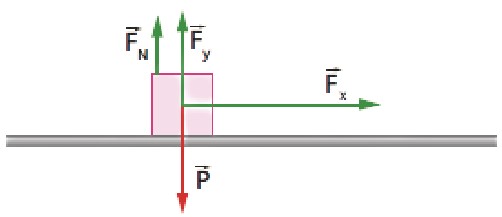
É nesse momento que percebemos se nossa hipótese de que o bloco não perde contato com o plano horizontal é ou não correta. O bloco perderia o contato se Fy > P. Mas, como podemos observar, neste caso temos Fy < P. Portanto, o bloco não perde o contato, o que significa que, na direção vertical, as forças devem se anular:
FN + FY = PFN + 50 = 150 ⇒ FN = 100 N
b) A força resultante é a força componente Fx→. Portanto:
Fx = m . a ⇒120 = 15 . a ⇒ a = 8, 0 m/s²




