SOM
O som se dá devido à sucessão de compressão e de rarefação das moléculas do meio:
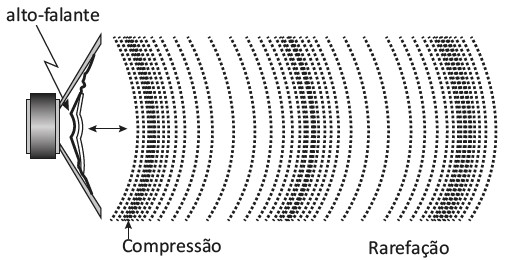
O comprimento de onda do som é a distância entre duas compressões (cristas) ou duas rarefações (vales). A sua velocidade depende da temperatura local. Quanto maior a temperatura, maior será a agitação molecular, consequentemente, maior será a sua velocidade, mas a relação não é linear. Quando o som se propaga nos gases (ideais), podemos dizer que a velocidade de propagação depende da temperatura (T, em Kelvin) e da massa molecular (mm) do gás.

QUALIDADES FISIOLÓGICAS DO SOM
ALTURA
Um som alto significa um som agudo. Já um som baixo, grave. Ou seja, a altura se relaciona com a frequência do som.
INTENSIDADE
A intensidade, conforme mensuramos anteriormente, depende do quadrado da frequência e da amplitude da onda. Ondas de mesma frequência serão mais fortes quanto maior forem as suas amplitudes, e mais fracas se possuírem amplitudes menores.
Uma pessoa que está mais afastada de uma caixa de som que uma outra pessoa escutará um som menos intenso, resultando em um menor nível sonoro (N).
Podemos medir a intensidade de uma onda também através da relação abaixo:

Em que P é a potência da fonte sonora e, A, a área varrida pelo som desde a fonte até o ouvinte. Como se trata de uma onda tridimensional (esférica):
A = 4πd²
Em que d é a distância do ouvinte à fonte.
A unidade padrão de intensidade é W/m2.
Exemplo: A 125 m da casa de Edgar está acontecendo uma festa com uma caixa de som de 2 kW de potência. Se Edgar possuísse um decibelimetro (aparelho que mede nível sonoro), qual seria a sua marcação?
Resolução: Para medirmos o nível sonoro, temos que calcular a intensidade sonora na casa do Edgar:

Substituindo o valor acima na equação de nível sonoro, obteremos:

Ruídos sonoros próximos a 120 dB começam a causar dor nos nossos ouvidos. Como estamos falando de uma escala logarítmica, há uma diferença grande entre 100 dB e 120 dB (no primeiro caso a intensidade é de 0,01 W/m², já no segundo, é de 1 W/m²). Porém um barulho da ordem de 100 dB é bem desconfortável se estivermos procurando dormir (equivale a barulho de trânsito, dentro de um ônibus ou trem).
A intensidade mínima que o ouvido de um humano capta um som é de 10-12 W/m². Portanto, a intensidade sonora para uma pessoa que está a uma distância x de uma caixa de som é 4 vezes maior que para uma pessoa que está a 2x da mesma fonte, o que não significa que o som será 4 vezes maior. Os nossos ouvidos, assim como os nossos olhos, funcionam em escalas logarítmicas. Para o som:

Unidade: dB (decibels).
TIMBRE
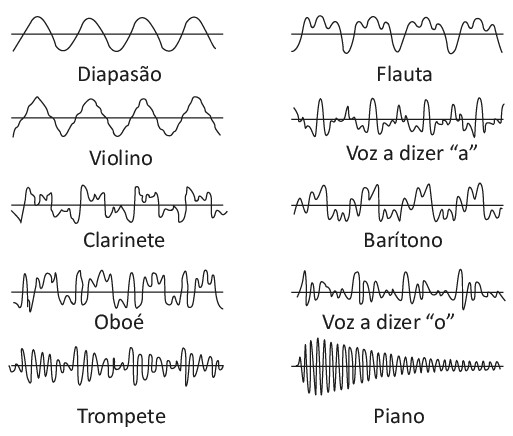
Sons de mesma frequência e amplitude podem ser diferenciados pela fonte emissora. Cada pessoa tem um timbre de voz único, assim como o som emitido por um violão é diferente de um emitido por um trompete. A figura abaixo mostra como são as ondas produzidas por diferentes instrumentos musicais, cada um com o seu timbre (propriedade sonora da fonte).
QUADRO COMPARATIVO ENTRE SOM E LUZ

CORDA VIBRANTE
Vamos imaginar um músico tocando um violão. Ao fazer uma corda vibrar, as moléculas no ar serão postas a vibrar também. A frequência de vibração da corda é a mesma que a frequência de vibração das moléculas do ar, ou seja, a corda vibra na mesma frequência que o som gerado pela sua vibração. A velocidade com que a corda se movimenta não é a mesma que a velocidade de propagação da onda sonora (a corda não vibra a 340 m/s, por exemplo).
fcorda = fsom
Para a corda vibrar na exata frequência que o músico deseja, duas grandezas são importantes: o tamanho da corda e a sua densidade (linear → devido à proporção, dizemos que as cordas têm apenas uma dimensão). Como a corda tem comprimento fixo, o músico a pressiona em um ponto, tornando o pedaço de corda vibrante o quanto menor ele queira. Por exemplo, ao pressionar a corda na sua metade, apenas a metade da corda irá vibrar. Além disso, as cordas de um violão possuem densidades diferentes, o que influencia na frequência de vibração. Cordas mais densas produzem sons mais graves.
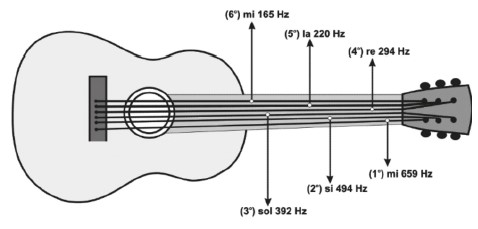
Vamos dizer que, quando uma corda de violão vibra, o som produzido será uma onda harmônica. Isso porque, ao vibrá-la em certo ponto, a corda estará sob M.H.S., ou seja, todos os pontos da corda que estão vibrando na vertical, por exemplo, tem o mesmo período, a mesma frequência conforme estudamos no módulo anterior.

A configuração mais simples possível (harmônico fundamental) de corda vibrante é a situação que estudamos. Perceba, pelo formato da onda, que o comprimento total da corda L equivale à metade do comprimento de onda λcorda, que vamos chamar apenas de λ. Logo:
L = λ/2
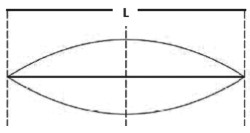
Então:

Essa é a frequência de vibração da corda no harmônico fundamental. Como sabemos, v é a velocidade de propagação da corda, e L, o seu comprimento. Usando a equação de Taylor, podemos chegar a uma relação mais geral de frequência:

Agora veja a configuração do 2° harmônico:
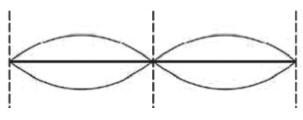
Nesse caso, o comprimento de onda na corda é igual ao seu comprimento L. Então:

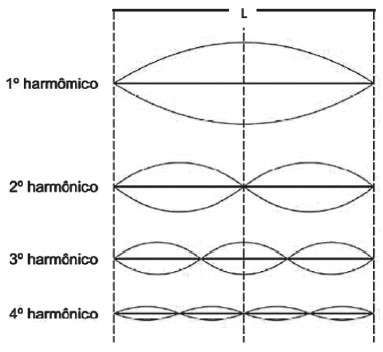
Já no 3° harmônico, 1,5 λ. Então:

Vistos os três casos acima, podemos perceber a expressão mais geral de frequência em cordas:

E, se ao invés de uma corda, tivéssemos um tubo completamente aberto nas duas extremidades, deixando um som se propagar em seu interior?
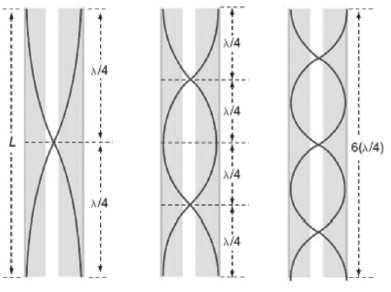
Perceba que a relação entre o comprimento de tubo L e o comprimento de onda do som λsom segue a mesma que a relação anterior entre o comprimento da corda e a onda nela formada após ser posta em vibração. Então, em tubos abertos, podemos escrever que:

Em que v é a velocidade de propagação da onda sonora no interior do tubo e n é o número do harmônico. n = 1 significa harmônico fundamental, n = 2, 2° harmônico e assim sucessivamente.
O que acontece se fecharmos uma das extremidades?
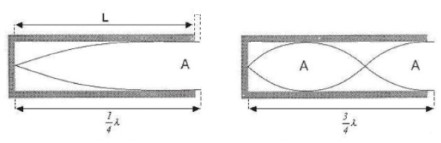
Esse tipo de tubo, com uma das extremidades fechada, é chamado de tubo fechado. Nesse tubo, o som será refletido na extremidade fechada.
Acima temos a configuração mais simples (harmônico fundamental) desse caso. Nessa situação, temos apenas ¼ do comprimento de onda do som dentro do tubo, logo:

Já na situação abaixo, temos o próximo harmônico, com ¾ do comprimento de onda no tubo.

Vamos fazer o harmônico seguinte, para acharmos uma relação:

Na figura acima, vemos que 5/4 λ estão no tubo. Logo:

Então, em tubos abertos, podemos escrever que:

Observação: Como n é o número do harmônico, note que, no caso de tubos sonoros fechados, não há harmônicos pares, apenas ímpares (n = 1,3,5,…).
Vamos imaginar a seguinte situação: três copos com níveis de água diferentes. Um copo com 25% de água, o outro com 50% e o último com 75%. Batendo no copo com uma colher, um som será produzido e propagado no interior do copo. Sendo assim, cada copo produzirá um som com frequência diferente. Considerando que o som produzido estava no harmônico fundamental nos três casos, note que:

No 1° tubo, como há 25% de água, o som pode se propagar nos outros 75%, ¾ L. Já no 2° tubo, o som terá L/2 para se propagar e, no 3°, L/4.




