2ª Lei da termodinâmica

As tentativas de melhorar os rendimentos das máquinas térmicas tem tudo a ver com as perguntas acima. Carnot, em 1824, antes mesmo da formulação da 1ª lei (meados de 40), debruçou-se diante desse problema. Seus estudos ajudaram na formulação da 2ª lei de Clausius (1850) e Kelvin (1851).  

ENUNCIADOS DA 2ª LEI DA TERMODINÂMICA

Kelvin: é impossível realizar um processo cujo único efeito seja remover calor de um reservatório térmico e produzir uma quantidade equivalente de trabalho.

Observação: Perceba que isso não significa que é impossível converter calor inteiramente em trabalho, como muitos autores escrevem! É possível converter todo calor em trabalho. Por exemplo, um gás em processo de expansão isotérmica. Sua variação de energia interna é zero, portanto, todo calor absorvido se converteu em trabalho (τ = Q).  

Quando Kelvin disse único efeito, significa que o sistema tem que voltar ao estado inicial, ou seja, que o processo é reversível (cíclico). No exemplo acima, da expansão isotérmica, não há contradição ao enunciado de Kelvin, já que o estado inicial se difere do final. Ou seja, para processos reversíveis, considerando um ciclo completo, é impossível converter todo calor em trabalho.

Se pudéssemos ter um ciclo em que o calor se transformasse completamente em trabalho, teríamos um motor perpétuo, violando a 1ª lei. Para termos uma máquina térmica operando em ciclos, é necessário o fornecimento de calor.

Clausius: é impossível realizar um processo cujo único efeito seja transferir calor de um corpo mais frio para um corpo mais quente.

Lembrando que, novamente, aparece a expressão único efeito, ou seja, o processo deve ser cíclico. Se o gás não voltar para o estado inicial, é possível. Por exemplo, podemos colocar um recipiente contendo um gás em contato com um corpo mais frio, que pode absorver calor desse gás caso sofra um processo de expansão isotérmica (∆U = 0, Q = τ > 0). Em seguida, o gás pode sofrer uma compressão adiabática, até atingir uma temperatura maior que na etapa anterior (essa temperatura mais baixa da etapa anterior é a mesma que o corpo tem, já que estava em contato com o gás). Colocando novamente esse gás em contato com o corpo, que está a uma temperatura mais baixa que gás, o gás pode receber calor por compressão isotérmica (∆U = 0, Q = τ < 0). Nada impede que o trabalho total seja zero e o estado final seja diferente do inicial (sua temperatura aumentou) e recebeu calor de um corpo mais frio.

MÁQUINAS TÉRMICAS

Uma máquina térmica é um dispositivo capaz de converter energia interna em trabalho mecânico e foi a base da 1ª Revolução Industrial no final do século XIX. Esse trabalho é obtido somente quando o calor flui espontaneamente de uma região de maior temperatura (fonte quente) para uma região de menor temperatura (fonte fria) como descrito no esquema energético abaixo:

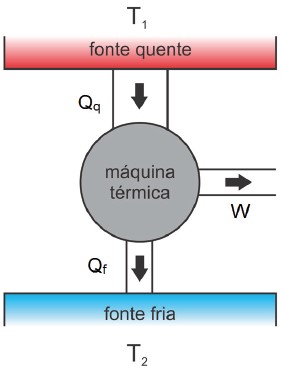
Existem três grandezas energéticas representadas:

• Fonte quente: regiões a altas temperaturas (uma caldeira com vapor d’água, por exemplo) que fornecem calor (Qq) para a máquina.
• Fonte fria: regiões para onde o excesso de calor (Qf) é rejeitado.
• Trabalho: energia aproveitada para realizar alguma tarefa útil (W).

Para que o equipamento funcione, há um gás que sofre uma transformação cíclica, ou seja, ele começa em um estado inicial A, vai para outros estados e depois retorna ao estado A. Na representação de um diagrama P×V, teremos uma superfície fechada com os pontos inicial e final conincidentes. A área destacada, “interna” à curva, nos fornece o trabalho realizado pelo gás durante a transformação.

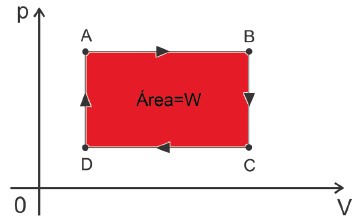
Observação: 

• Como não há variação de temperatura ao final do ciclo: ∆Uciclo = 0.
• O ciclo de uma máquina térmica estará sempre no sentido horário.

Usando a 1ª lei da termodinâmica ao longo do ciclo, temos:

∆U = Q – W = 0

Q = W

Também podemos observar pelo balanço energético que:

Q_q = Q_f + WQ_q – Q_f = Q = W

RENDIMENTO

A segunda lei da termodinâmica (que será abordada mais a frente) nos garante que nenhuma máquina térmica pode converter todo o calor que lhe é fornecido em energia mecânica. Assim, há um aproveitamento parcial do calor ao ser transformado em trabalho chamado de rendimento η e pode ser calculado por duas expressões:

Observação: O rendimento de qualquer máquina térmica é sempre menor que 100%: η < 1

Exercício Resolvido 1: Durante cada ciclo, uma máquina térmica absorve 500 J de calor de um reservatório térmico, realiza trabalho e rejeita 420 J para um reservatório frio. Para cada ciclo, o trabalho realizado e o rendimento da máquina térmica são, respectivamente, iguais a  

a) 80 J e 16%

b) 420 J e 8%

c) 420 J e 84%

d) 80 J e 84%

Resolução: A

Da 1ª Lei da Termodinâmica:

Curiosidade: No final do século XVIII, o escocês James Watt criou um dispositivo eficiente que convertia calor em trabalho mecânico. A partir daí, a burguesia fez grandes investimentos e sua máquina foi empregada em moinhos, bombas d’água, locomotivas, barcos a vapor e em fábricas, sendo um dos principais fatores que levaram à Revolução Industrial.

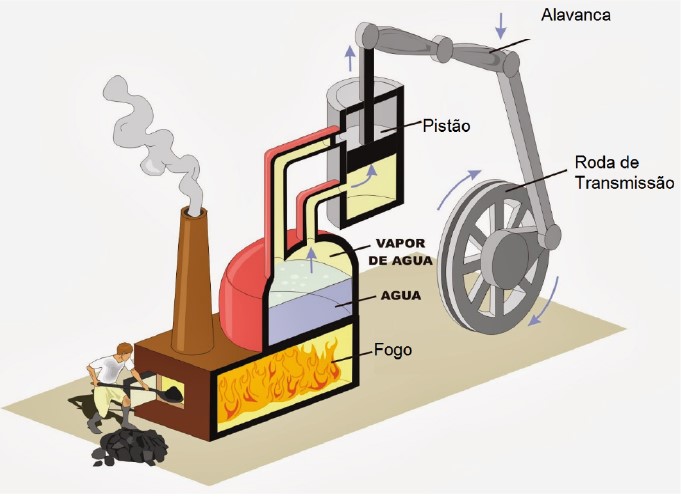
MOTORES DE COMBUSTÃO INTERNA

Os motores de combustão interna são máquinas térmicas usadas em veículos, exceto os elétricos. Eles possuem um ciclo de queima de combustível para produção de calor e movimento de pistões para realizar trabalho. Vamos ilustrar alguns exemplos:

CICLO OTTO (1876)

Esse é o ciclo dos motores movidos à gasolina e possui 4 tempos (transformações).

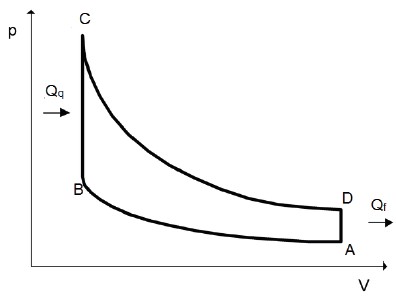
• Começando em O, o combustível e o ar são admitidos no pistão; o ciclo térmico ainda não começou.
• A partir de A, o gás é comprimido adiabaticamente até o ponto B.
• Aquecido isometricamente até o ponto C pela fonte quente.
• Expandido adiabaticamente até o ponto D.
• Resfriado isocoricamente até retornar ao ponto A.

Durante o processo de AB, há um fator de compressão dado pela razão entre o volume inicial do pistão e seu volume quando comprimido, ou seja, r = ^VA/_VB. Esse fator que determina o rendimento do motor à gasolina:

CICLO DIESEL (1900)

Esse é o ciclo dos motores movidos à diesel e também possui 4 tempos (transformações).

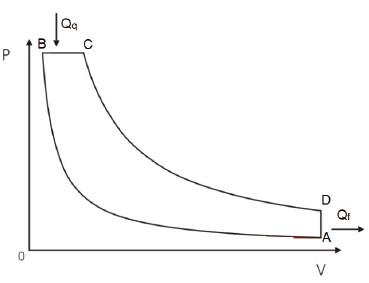
• Começando no ponto A, o gás é comprimido adiabaticamente até o ponto B.
• Aquecido isobaricamente até o ponto C pela fonte quente.
• Expandido adiabaticamente até o ponto D.
• Resfriado isocoricamente até retornar ao ponto A.

CICLO DE CARNOT

Em 1824, o engenheiro francês Nicolas Léonard Sadi Carnot, analisando o funcionamento das máquinas térmicas, descobriu qual a fração máxima de calor que poderia ser convertida em trabalho. Ou seja, qual o rendimento máximo que uma máquina poderia ter. Essa máquina ideal tem rendimento dado por:

Observação: As temperaturas precisam estar sempre na escala absoluta Kelvin.

E seu ciclo termodinâmico contém 4 etapas que você precisa saber:

• Expansão isotérmica AB na temperatura T_q, absorvendo Q_q de calor.
• Expansão adiabática BC até a temperatura T_f.
• Compressão isotérmica BD na temperatura T_f, rejeitando Q_f de calor.
• Compressão adiabática DA até a temperatura retornar para T_q.

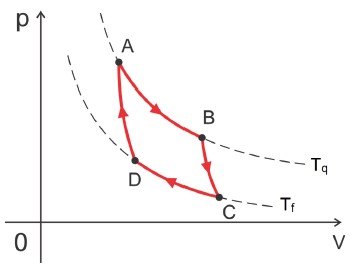
Diagrama P×V do Ciclo de Carnot

Somente nesse ciclo, vale a relação:

Observação: Essa máquina hipotética mostra qual o rendimento máximo de uma máquina térmica que opera entre as temperaturas T_q e T_f. Assim para qualquer máquina térmica real vale a relação:

0 < η_máquina < η_Carnot < 1

Exercício Resolvido 2: Uma máquina a vapor foi projetada para operar entre duas fontes térmicas, a fonte quente e a fonte fria, e para trabalhar segundo o ciclo de Carnot. Sabe-se que a temperatura da fonte quente é de 127°C e que a máquina retira, a cada ciclo, 600 J desta fonte, alcançando um rendimento máximo igual a 0,25. O trabalho realizado pela máquina, por ciclo, e a temperatura da fonte fria são, respectivamente:

a) 240 J e 95°C

b) 150 J e 27°C

c) 15 J e 95°C 90 J e 27°C

d) 24 J e 0°C

Resolução: B

REFRIGERADORES

Um refrigerador é um dispositivo capaz de fazer o calor fluir da fonte fria para a fonte quente. No entanto, esse processo não é espontâneo e necessita do gasto de energia mecânica (trabalho) para que ele funcione. O diagrama energético de um refrigerador está representado na figura abaixo:  

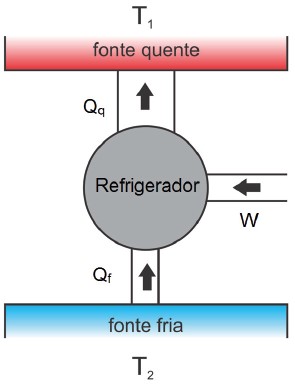
Observação:

• Um refrigerador também sofre um processo cíclico, porém no sentido anti-horário
• Como não há variação de temperatura ao final do ciclo: ∆U_ciclo = 0.

Da primeira lei da termodinâmica, temos:

ΔU = Q – W = 0 ⇒ Q = WQ_q = Q_f + W ⇒ Q_q – Q_f = Q = W

EFICIÊNCIA

O objetivo do refrigerador é retirar calor da fonte fria gastando energia mecânica (trabalho) no processo. Assim um bom refrigerador retira a maior quantidade possível de calor e consumindo a menor quantidade de trabalho. A razão entre essas duas grandezas mede a sua eficiência.

Observação: Em algumas questões, a eficiência também pode ser chamada de rendimento e vice-versa.

Exemplo: Geladeira e ar condionado são os aparelhos refrigerantes mais comuns.

REFRIGERADOR DE CARNOT

Existe um refrigerador que possui máxima eficiência, chamado de refrigerador de Carnot. Essa eficiência pode ser calculada pela seguinte expressão:

Exercício Resolvido 3: Um refrigerador foi construído, utilizando-se uma máquina de Carnot cuja eficiência, na forma de máquina de calor, é igual a 0,1. Se esse refrigerador realiza um trabalho de 10 J, é CORRETO afirmar que a quantidade de calor removida do reservatório de menor temperatura foi, em joules, de

a) 100

b) 99

c) 90

d) 10

e) 1

Resolução: C

A eficiência de um refrigerador é dada pela relação entre a quantidade de calor retirada do congelador (Qfrio) que é a fonte fria e o trabalho (W) recebido do sistema motor-compressor. No caso, como o enunciado refere-se a uma máquina de calor, deve-se inverter a relação, como uma máquina térmica motora.

Mas, na máquina motora:

Q_quente = W + Q_frio ⇒ 100 = 10 + Q_frio ⇒ Q_frio = 100 – 10Q_frio = 90 J

ENTROPIA, UMA ANÁLISE MACROSCÓPICA

A entropia é uma função de estado associada ao equilíbrio termodinâmico. Todo sistema tende a evoluir naturalmente para um estado de menor energia e maior entropia. Assim, como a 1ª lei da termodinâmica corresponde à existência da função de estado energia interna, a 2ª lei nos leva à entropia.

Para entendermos o que vem a ser essa grandeza, vamos voltar ao ciclo de Carnot. Levando o sinal negativo, do calor liberado para a fonte fria, em consideração, de modo mais correto, podemos escrever, para um ciclo de Carnot, que:

Em um ciclo reversível qualquer, como sabemos, todas as trocas de calor devem ser feitas sob temperaturas constantes. Então, podemos expandir a equação acima para qualquer ciclo reversível. Vamos chamar de dQ uma troca de calor infinitesimal. Sendo assim, obtemos o teorema de Clausius:

Vamos analisar o ciclo reversível abaixo:

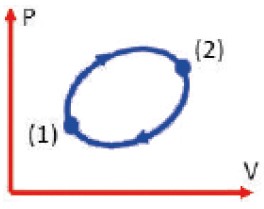
Usando o teorema de Clausius, temos que:

Podemos concluir que essa integral é independente do caminho. A grandeza equivalente a essa integral é, portanto, uma função de estado. É equivalente à grandeza energia potencial e energia interna. A grandeza equivalente à integral acima é a variação de entropia (∆S):

Unidade (S.I.): J/K.

Vamos aprender a calcular a variação de entropia (assim como a energia potencial, o nosso objetivo é calcular a sua diferença, e não o valor absoluto).

TRANSFORMAÇÃO ADIABÁTICA REVERSÍVEL

Como não há troca de calor nesse caso, não teremos variação na entropia do sistema.

dQ = 0 ∴ ∆S = 0

Essa transformação também é chamada de isentrópica (entropia constante).

MUDANÇA DE FASE

O que acontece com a entropia durante um processo de liquefação ou vaporização, por exemplo? Nesses casos, não há mudança na temperatura. Sendo assim:

O sinal será positivo se for fusão ou vaporização, e será negativo se for liquefação ou solidificação.  

Exercício Resolvido 4: Qual é a variação de entropia de 1 g de água a 100 °C, sofrendo uma vaporização?

Resolução:

FLUIDO INCOMPRESSÍVEL

Supondo um líquido que sofresse uma variação de temperatura a volume constante. Supondo o calor específico do fluido constante durante essa variação de temperatura, temos que:

Exercício Resolvido 5: 200 ml de água receberam calor de uma fonte quente, aumentando a sua temperatura de 20 °C para 60 °C. Qual foi a variação de entropia sofrida pelo líquido (incompressível)?

Resolução:

EXPANSÃO LIVRE

Como já vimos, não é um processo reversível. Para calcularmos a variação de entropia nesses casos de processos irreversíveis, como a variação de entropia só depende do estado inicial e final, seu valor será o mesmo, quer o processo que passe por esses estados seja irreversível ou reversível. Para a vizinhança do sistema, a variação de entropia não será a mesma para esses casos, mas, para o sistema em si, é.

No caso da expansão livre, podemos imaginar uma transformação isotérmica. Sendo assim:

Voltando ao nosso exemplo inicial do frasco de perfume: quando destampamos o frasco, o cheiro do perfume se espalha. Como sabemos, esse processo de difusão é irreversível.

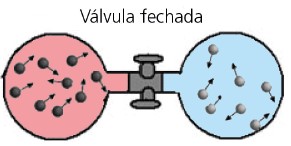
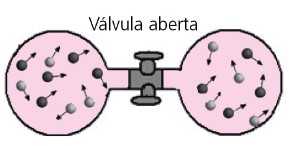
No exemplo acima, por exemplo, após a abertura da válvula, haverá uma mistura homogênea dos dois gases ocupando todo o volume possível. Podemos pensar que os dois gases sofrem expansões livres cujo volume final é o dobro do inicial. Usando a equação acima:

Como diferenciar o processo reversível de um irreversível apenas pela entropia? Simples, em um processo que acontece em um sistema fechado, a entropia do sistema aumenta para processos irreversíveis e fica constante para processos reversíveis. A entropia nunca diminui.

∆S ≥ 0

Observação: O sistema fechado, quando levado em consideração as suas vizinhanças, chamamos de universo. É comum, em questões de concursos, considerarem que a variação de entropia de um sistema pode ser negativa, considerando sistema como um gás, por exemplo. Mas, a variação de entropia do gás mais a variação de entropia do reservatório e do ambiente ao seu redor, ou seja, a variação de entropia do universo, será sempre maior que zero.