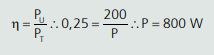Vamos imaginar que temos um livro em cima de uma mesa, em repouso em relação ao solo. Para que o livro comece a se deslocar em relação ao solo, deve sofrer a ação de uma força externa. Como a velocidade de corpo varia com a ação de uma força externa, dizemos que esse corpo está sofrendo uma variação de energia. Podemos imaginar também um carro em movimento. É a força gerada pelo motor que faz a velocidade do carro aumentar, aumentando, consequentemente, a sua energia. Quando os freios são acionados, o atrito entre o pneu e o asfalto faz a velocidade diminuir, ou seja, a energia do carro começa a diminuir.
Quando um agente externo realiza uma força sobre um sistema, fazendo com que a velocidade do sistema sofra variações, dizemos que esse agente externo está realizando um trabalho (W) sobre o sistema.
Essa variação de velocidade pode ser traduzida como variação de energia (cinética) do sistema. A energia total de um corpo chama-se energia mecânica (E), que é a soma de duas outras energias: energia potencial (Ep) e energia cinética (Ec):
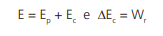
Ou seja, energia cinética é a que muda quando há um trabalho sendo realizado pelo sistema (W > 0) ou sobre o sistema (W < 0). Supondo que haja n forças atuando em um corpo, se a velocidade aumentar, o trabalho resultante (Wr ) é positivo, se diminuir, é negativo. Essa equivalência entre trabalho e energia cinética é chamada de teorema trabalho – energia.
Energia cinética de um corpo de massa m:

Ou seja, trabalho é uma grandeza escalar.
Atenção
A unidade de energia do S.I. é J (Joule).
Exercício Resolvido
01. Uma bolinha de 2 kg é abandonada a uma altura de 5 m. Desprezando a resistência do ar, responda as perguntas abaixo:
a) Qual a variação de energia cinética da bolinha do instante
inicial até o momento em que toca no solo?
b) Qual a velocidade final da bolinha?
Resolução:
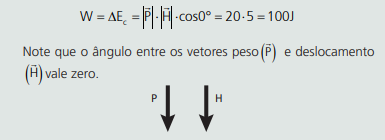
a) A variação de energia cinética corresponde ao trabalho da força resultante. Como a única força que atua no corpo é a força peso, podemos dizer que:
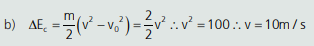
Exercício Resolvido
02. Um bloco de pedra, de 40 kg, desce um plano inclinado a partir do repouso, deslizando sobre rolos de madeira, sem atrito.
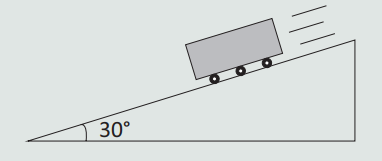
Sabendo-se que o plano inclinado mede 12 m, calcule o trabalho resultante das forças que atuam no bloco.
Resolução:
As forças que atuam no bloco são peso e normal. Como a normal é perpendicular ao vetor deslocamento, ela não irá realizar trabalho (a normal não altera o módulo da velocidade do bloco). Então, a força responsável pela variação da velocidade é a força peso.
Temos que:
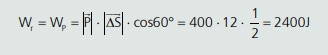
E se o bloco fosse abandonado na altura do plano inclinado (H =12/sen30° = 6 m), qual seria o trabalho resultante?
Nesse caso a única força atuante é o peso. Então:
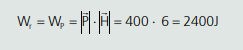
O que podemos concluir com isso? Algo notável. Não importa a trajetória do corpo, a variação da sua energia cinética e, consequentemente, o trabalho resultante, só dependem do desnível (altura) entre as suas posições inicial e final:
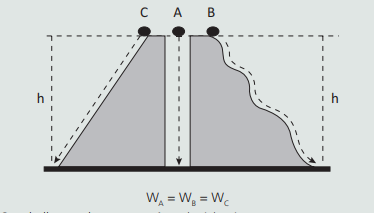
O trabalho resultante nas três trajetórias é o mesmo. Esses sistemas sem atuação de forças dissipativas (atrito, resistência do ar) são chamados de sistema conservativos. A energia mecânica do corpo é constante durante a trajetória. Conforme o corpo ganha velocidade (energia cinética), perde energia potencial.
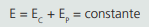
ENERGIA POTENCIAL DE UM CORPO DE MASSA M
Vamos estudar ao longo do curso três tipos de energias potencias: gravitacional, elástica e elétrica. Quando estiver falando de um corpo de massa m sofrendo um desnível h, sofrerá uma variação de energia potencial gravitacional.
Vamos pegar o exemplo da situação anterior, dos corpos A, B e C caindo de uma altura h. A velocidade inicial dos corpos era zero. Então, inicialmente, suas energias mecânicas valiam:
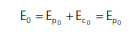
Como é um sistema conservativo, a energia total se conserva, ou seja:
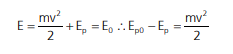
A energia potencial não tem um valor fixo. Não podemos calcular a energia potencial de um ponto, mas podemos medir a variação de energia potencial entre dois pontos. O que se faz nos exercícios é escolher um ponto para a energia potencial ser zero, e aí, achar a energia em outro ponto qualquer. Mas, de fato, o que calculamos é a sua variação.
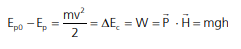
Exercício Resolvido
03. Uma bolinha de massa 80 g é arremessada do solo e alcança uma altura de 5 m, em relação ao solo. Qual foi a sua variação de energia potencial gravitacional?
Resolução:
Como a energia mecânica é constante:
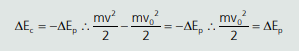
Usando Torricelli:
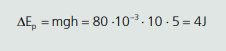
Com isso, conseguimos descobrir a sua velocidade inicial:
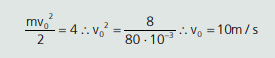
ENERGIA POTENCIAL ELÁSTICA
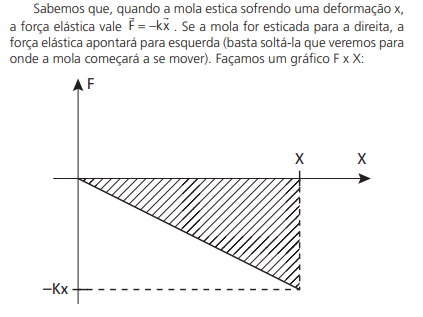
Quando um corpo está atado a uma mola/elástico, pode sofrer uma diferença de energia potencial elástica. Vamos imaginar um objeto preso a uma mola encolhida, em uma superfície horizontal. Ao soltar a mola, ela começará a se esticar, tendendo a voltar para a posição de equilíbrio. Durante esse movimento oscilatório, o objeto sofre variações de velocidade, ou seja, a sua energia cinética muda o tempo todo. A energia cinética mudando, há realização de trabalho. A força que faz a velocidade mudar é a força elástica (Fel):
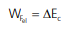
O problema é que, como a força elástica depende da deformação da mola, durante o movimento oscilatório, a força elástica muda a cada instante de tempo. Como fazer para medir o trabalho da força elástica?
A cada infinitésimo de deslocamento da mola, temos uma força elástica. Quanto melhor esse deslocamento, mais precisa será a força elástica instantânea. Somando todos os infinitésimos de trabalho teremos:
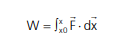
Para forças constantes:
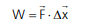
Mas, no caso de forças que dependem de x (F = F(x)), teríamos que resolver a integral acima. Porém, conforme já discutimos em cinemática, basta calcularmos a área do gráfico F × x. A área nada mais é do que a própria integral. Então, pelo gráfico, temos que:
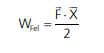
Em que x é a deformação da mola (seu deslocamento). Então:
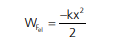
Usando o Teorema Trabalho – Energia:
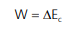
E, como estamos em um sistema conservativo:
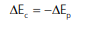
Temos a variação de energia potencial elástica quando um elástico é deformado de x valendo:
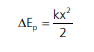
Exercício Resolvido
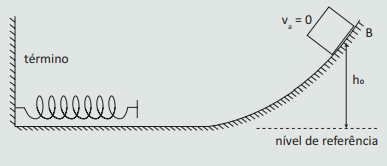
Um bloco de massa m parte do repouso a uma altura h0 em relação ao solo. Ao final do movimento, irá colidir com uma mola de constante elástica k. Qual será a máxima deformação sofrida pela mola?
Resolução:
Como é um sistema conservativo, a energia mecânica se conserva, ou seja, conforme o bloco vai caindo, como a sua energia cinética vai aumentando, podemos inferir que sofre uma queda de energia potencial gravitacional. Como o bloco é parado pela mola, toda a sua energia cinética é reduzida a zero, indicando que o sistema massa-mola vai ganhando energia potencial elástica. Logo:
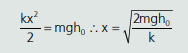
SISTEMAS NÃO CONSERVATIVOS
Um homem descendo de paraquedas e um carro que freia são exemplos de sistemas que a energia mecânica diminui com o tempo, ou seja, há dissipação de energia. A força que o vento faz no paraquedas faz com que a velocidade de queda seja praticamente constante durante um certo período, ou seja, o homem perde energia potencial (está caindo), mas a cinética fica constante, portanto sofre perda de energia mecânica. No caso do carro, a força de atrito dissipa energia cinética do sistema.
No 1° caso, então, o trabalho do peso é igual, em módulo, ao trabalho da força do vento. Como não há variação de energia cinética, o trabalho total é nulo. Então:

Já no 2° caso, o trabalho da força de atrito é igual à variação de energia cinética do carro:
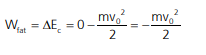
POTÊNCIA
A grandeza potência (P) de um elemento (motor, por exemplo) mede o módulo da variação de sua energia a cada intervalo de tempo
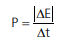
Unidade de potência do S.I. : W (Watts).
Vamos estudar três tipos de potências: mecânica, térmica e elétrica.
POTÊNCIA MECÂNICA
É a potência exercida por uma força motriz ou por uma força dissipativa em um corpo de massa m.
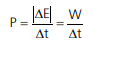
Exercício Resolvido
05. Um guindaste faz com que um corpo de massa 1,0 tonelada suba uma altura de 2,4 m em 2 minutos, com velocidade constante. Qual a potência do motor (ideal) do guindaste?
Resolução:
Como o corpo sobe com velocidade constante, podemos inferir que o módulo do vetor peso é igual ao da força que o motor faz para levantá-lo (podemos pensar que há um cabo puxando-o, sendo assim, a tração seria a força motriz).
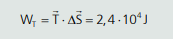
Então, a potência do motor será:
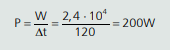
Repare que colocamos o intervalo de tempo em segundos (S.I.).
Observação
Para deslocamentos com velocidade constante, podemos ver que:
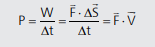
Perceba que potência também é uma grandeza escalar.
POTÊNCIA TÉRMICA
É o calor liberado para um sistema em um intervalo de tempo.
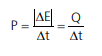
A unidade do S.I. continua sendo W, que equivale a J/s. Porém, nesse tipo de assunto, é comum a unidade cal/s ou Kcal/s. Lembrando que 1 cal ≈ 4,18 J.
Exercício Resolvido
06. Um micro-ondas cuja potência vale 800 W é usado para aquecer 200 ml de água de 20 °C até 100 °C. Considerando que o sistema está no nível do mar, qual é o intervalo de tempo necessário para que a água sofra essa variação de temperatura?
Resolução:
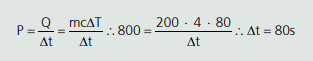
Usamos 1 cal = 4 J, calor específico da água valendo 1 cal/g°C, ou seja, 4 J/g°C, e sua densidade 1g/cm³.
LEITURA OPCIONAL
ENERGIA POTENCIAL ELÉTRICA
Uma partícula eletrizada, livre de atuação de quaisquer outras forças, sofre variação de energia cinética quando submetida a uma região de atuação de um campo elétrico (E). Qual força realiza trabalho sobre a partícula? Ao entrar em uma região com campo elétrico, uma partícula carregada eletricamente sofre uma força chamada de força elétrica (FE). Podemos dizer que:
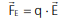
Sabemos também que:
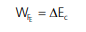
Para haver campo elétrico, a região deve estar submetida a uma diferença de potencial (U). Quando temos um campo elétrico uniforme E em um local, quanto maior a distância entre dois pontos, maior será a d.d.p., ou seja:
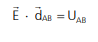
Combinando as três equações, teremos:

A variação de velocidade da partícula só depende das suas posições finais e iniciais, e não da trajetória.
Exercício Resolvido
07. Um elétron sofre um d.d.p. de 100 V. Sabendo-se que partiu praticamente do repouso, qual será a sua velocidade final?
Resolução:
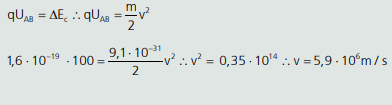
POTÊNCIA ELÉTRICA
É a energia elétrica gerada/consumida por um ou mais elemento(s) de um circuito em um intervalo de tempo. Também podemos nos referir à potência elétrica quando uma partícula sofre uma d.d.p., mudando a sua energia cinética. Sendo assim, o trabalho da força elétrica por intervalo de tempo também é potência elétrica. Nos circuitos, os elétrons se locomovem, sofrendo uma d.d.p. De fato, as
duas definições são equivalentes.
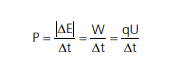
A quantidade de carga q que passa em um fio em um intervalo de tempo chama-se corrente elétrica (i):

Ou seja, a potência elétrica de um elemento de um circuito só depende da corrente que passa neste elemento e da d.d.p. que o elemento está submetido.
Vamos discutir esse assunto com maior clareza em circuitos elétricos.
Exercício Resolvido
08. Quando uma corrente elétrica passa por um resistor (R), parte de sua potência elétrica vira térmica. Isso se chama Efeito Joule. Suponha que um chuveiro elétrico sob d.d.p. de 220 V faz com que a água que estava na caixa d’água a 25 °C fique a 35 °C. Isso acontece porque, quando a água passa pela resistência elétrica dentro do chuveiro, ela aquece rapidamente a água. Sabendo-se que a vazão do chuveiro é de 3 litros por minuto, qual será a potência do chuveiro?
Resolução:
A potência elétrica absorvida pelo resistor vira integralmente térmica nesse exemplo (o que, na prática, é impossível). Então:

Vazão (z), como a questão informa, é a variação de volume de certo líquido por unidade de tempo:
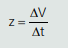
Como a densidade (ρ) de um líquido é a relação entre a sua massa e o seu volume:
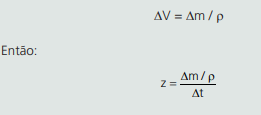
Nesse caso, dizer que 3 l de água passam por minuto significa dizer que 3 kg de água passam por minuto no chuveiro, ou seja:
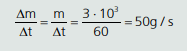
Em que a variação de massa que passa pelo chuveiro é equivalente a massa m aquecida pelo mesmo. Agora (usando 1 cal = 4J):
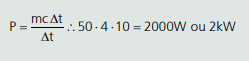
OBSERVAÇÃO:
Perceba que, diminuindo a vazão do chuveiro a variação de temperatura da água é maior, já que a sua potência é constante. Conclusão, para tomar banho quente em chuveiro elétrico, devemos fechar um pouco a torneira. Pouca vazão, água quentinha.
Para acharmos a corrente que passa no circuito do chuveiro:
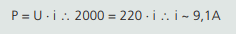
RENDIMENTO
Nenhum motor tem 100% de rendimento (η), ou seja, a potência útil será sempre menor que a potência nominal ou total. O rendimento é a relação entre a potência útil e a nominal.
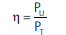
Exercício Resolvido
Vamos voltar ao nosso guindaste que levantou 1 tonelada a 2,4 m de altura em 2 minutos. Se o motor tivesse um rendimento de 25%, qual seria a sua potência nominal?
Resolução:
Achamos que a potência útil foi de 200 W. Então, a sua potência nominal vale 800 W. Apenas 1/4 é aproveitado: