SEQUÊNCIAS
Antes de começarmos o estudo das progressões, veremos uma definição um pouco mais geral: estudaremos o que é uma sequência.
Intuitivamente, uma sequência é uma lista de elementos que estão escritos em uma determinada ordem.
Formalmente, uma sequência é uma função cujo domínio é o conjunto dos números inteiros positivos.
Vejamos alguns exemplos de sequências:
I. 1, 2, 3, 4, 5, 6, … (sequência (infinita) dos inteiros positivos);
II. 2, 4, 6, 8, 10, … (sequência (infinita) dos inteiros positivos pares);
III. 2, 3, 5, 7, 11, 13, 17, … (sequência (in nita) dos números primos positivos);
IV. 5, 10, 15, 20, 25 (sequência ( nita) dos inteiros positivos múltiplos de 5 que são menores que 30);
V. 1, 1, 2, 3, 5, 8, 13, 21, …. (sequência (in nita) de Fibonacci – cada termo, a partir do segundo, é a soma dos dois termos anteriores).
Uma notação muito útil para representar sequências é a seguinte:
a1 representa o primeiro termo da sequência;
a2 representa o segundo termo da sequência;
a3 representa o terceiro termo da sequência;
…
an representa o n-ésimo termo da sequência.
Com efeito, no exemplo V, teríamos:
a1
= 1, a2
= 1, a3
= 2, a4
= 3, a5
= 5, a6
= 8, a7
= 13, a8
= 21
PROGRESSÃO ARITMÉTICA (PA)
Agora que já vimos o que é uma sequência, estamos aptos para introduzir a nossa primeira progressão.
Antes de mais nada, veja o seguinte exemplo: a Copa do Mundo da França ocorreu em 1998, a Copa do Mundo da Coreia do Sul e do Japão ocorreu em 2002, a Copa do Mundo da Alemanha ocorreu em 2006, a Copa do Mundo da África do Sul ocorreu em 2010 e a última Copa do Mundo, realizada no Brasil, ocorreu em 2014. Repare que a
Copa do Mundo acontece de 4 em 4 anos. Pela definição que veremos a seguir, os anos em que ocorrem a Copa do Mundo formam uma progressão aritmética.
DEFINIÇÃO
Uma sequência a1
, a2
, a3 , … é dita uma PROGRESSÃO ARITMÉTICA
(PA) se a diferença entre quaisquer dois termos consecutivos é constante, isto é, se a a r n n 1 , para todo n inteiro positivo e onde r é uma constante. Neste caso, dizemos que r é a razão desta PA.
Exemplos:
I. 1,1,1,1,1 é uma progressão aritmética com 5 termos e cuja
razão é igual a 1 – 1 = 0.
II. 1,2,3,4,5,6,… é uma progressão aritmética in nita com razão
1. III. 1 1
2
0 1
2
1 3
2 , , , , − − ,− é uma progressão aritmética com 6 termos e cuja razão é − 1 2 .
CLASSIFICAÇÃO
CRESCENTES: aquelas onde cada termo é maior que o anterior, ou seja, onde a razão é positiva.
Exemplo:
1,2,3,4,5,6,…
CONSTANTES: aquelas onde cada termo é igual ao anterior, ou seja, aquelas PA’s com razão nula.
Exemplo:
1,1,1,1,1
DECRESCENTES: aquelas onde cada termo é menor que o anterior, ou seja, onde a razão é negativa.
CONDIÇÃO PARA QUE 3 TERMOS EM SEQUÊNCIA FORMEM UMA P.A.
n1 n n1 n1 n n n1 (…,a ,a ,a ,…) a a a a −+ + ⇒ −=− − ⇒
n1 n1
n n1 n1 n
a a 2a a a a
2
+ −
+ −
+ = + ⇒=
Exemplo:
Encontre o valor de x para que os termos (x + 1, 2x – 3, 4x – 2)
formem, nessa ordem, uma progressão aritmética.
(x 1,2x 3,4x 2) (4x 2) (2x 3) (2x 3) (x 1)
4x 2 2x 3 2x 3 x 1 2x 1 x 4 x 5
( 4, 13, 22) r 9
+ − − ⇒ − − − = − − +⇒
− − + = − − − ⇒ + = − ⇒ =−
− − − ⇒ =−
4x 2 2x 3 2x 3 x 1 2x 1 x 4 x 5
( 4, 13, 22) r 9
− − + = − − − ⇒ + = − ⇒ =−
− − − ⇒ =−
TERMO GERAL
Vamos deduzir agora fórmulas para encontrar um termo de uma PA se conhecermos outro termo e a razão.
N-ÉSIMO TERMO EM FUNÇÃO DO PRIMEIRO
Como a diferença entre dois termos consecutivos é sempre igual à razão da PA, podemos escrever:






PROGRESSÃO GEOMÉTRICA (PG)
Veja a história a seguir:
“O grão-vizir, principal conselheiro do rei, tinha inventado um novo jogo. Era jogado com peças móveis sobre um tabuleiro quadrado que consistia em 64 quadrados vermelhos e pretos. O objetivo era capturar o rei inimigo, e por isso o jogo era chamado, em persa, shahmat – shah para rei, mat para morto. Morte ao rei. O jogo, claro, é o xadrez.
Mas reza a história que o rei cou tão encantado com a invenção que mandou o grão-vizir determinar sua própria recompensa. O grão-vizir já tinha a resposta na língua: era um homem modesto, disse ao xá.
Desejava apenas uma recompensa simples. Apontando as oito colunas e as oito las de quadrados no tabuleiro que tinha inventado, pediu que lhe fosse dado um único grão de trigo no primeiro quadrado, o dobro dessa quantia no segundo, o dobro dessa quantia no terceiro e assim por diante, até que cada quadrado tivesse o seu complemento
de trigo. Não protestou o rei, era uma recompensa demasiada modesta para uma invenção tão importante.
No entanto, quando o mestre do Celeiro Real começou a contar os grãos, o rei se viu diante de uma surpresa desagradável. O número de grãos começa bem pequeno: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024… mas quando se chega ao 64° quadrado, o número se torna colossal, esmagador. O número final chega a quase 18,5 quintilhões
(se cada grão tivesse o tamanho de um milímetro, todos os grãos juntos pesariam cerca de 75 bilhões de toneladas!).”
Este é um exemplo de progressão geométrica, que é o assunto que estudaremos a seguir.

CLASSIFICAÇÃO
CRESCENTES: aquelas em que cada termo é maior que o anterior.
DECRESCENTES: aquelas em que cada termo é menor que o anterior.
ALTERNANTES: aquelas em que cada termo possui sinal contrário ao do anterior.
CONSTANTES: aquelas em que cada termo é igual ao anterior.
ESTACIONÁRIAS: aquelas em que a razão é nula, ou seja, cada termo, a partir do segundo, é nulo.

TERMO GERAL
Vamos deduzir agora fórmulas para encontrar um termo de uma PG se conhecermos outro termo e a razão.
N-ÉSIMO TERMO EM FUNÇÃO DO PRIMEIRO
Podemos escrever:



PRODUTO DOS TERMOS DE UMA PG





SOMA DOS TERMOS DE UMA PAG
Não desenvolveremos aqui uma fórmula geral para o cálculo da soma dos termos de uma PAG, pois não é de grande valia guardar esta fórmula. O mais importante, na verdade, é saber o procedimento para se calcular a soma dos termos de uma PAG. Este procedimento é completamente similar ao método utilizado para o cálculo da soma
dos termos de uma PG.

PROGRESSÕES DE ORDEM SUPERIOR
Considere a seguinte imagem:
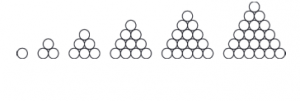
Contando o número de bolinhas em cada gura, temos:
• Figura 1 – 1 bolinha
• Figura 2 – 3 bolinhas
• Figura 3 – 6 bolinhas
• Figura 4 – 10 bolinhas
• Figura 5 – 15 bolinhas
• Figura 6 – 21 bolinhas
A sequência do número de bolinhas em cada gura é dada por 1, 3, 6, 10, 15, 21.
Agora, vamos observar as diferenças entre o número de bolinhas entre uma gura e a próxima:
3 – 1 = 2
6 – 3 = 3
10 – 6 = 4
15 – 10 = 5
21 – 15 = 6
Veja que a sequência formada por estas diferenças constitui uma progressão aritmética. Pela definição que veremos a seguir, a sequência do número de bolinhas em cada gura constituirá uma progressão aritmética de segunda ordem.

TERMO GERAL
Não demonstraremos o resultado a seguir neste material, pois a demonstração foge ao escopo dos concursos para os quais estamos nos preparando (a prova utiliza indução forte e algumas manipulações algébricas).
TEOREMA 1: O termo geral de uma PA de ordem k é um polinômio de grau k.
SOMA DOS TERMOS
Mais uma vez, não demonstraremos o resultado a seguir.
TEOREMA 2: A soma dos termos de uma PA de ordem k é um polinômio de grau k + 1, sem termo independente.
Vejamos agora um exercício resolvido:







