Neste módulo, começaremos nossos estudos da óptica geométrica, que engloba desde características da fonte luminosa até como se dá a propagação da luz em um objeto óptico (espelhos e lentes), entendendo os fenômenos de reflexão e refração luminosa.
A luz que sai de uma lâmpada, por exemplo, tem uma propagação isotrópica, ou seja, se propaga igualmente em todas as direções. Podemos entender a lâmpada como uma fonte pontual de luz que manda infinitos raios luminosos (RL) que se propagam no ambiente.
Se a dimensão da fonte for importante para o problema, falaremos que a fonte é extensa. Por exemplo, quando falamos de eclipses, a dimensão do Sol é de extrema importância, logo, trata-se de uma fonte extensa. Porém, quando estivermos falando de sombra projetada de um prédio em determinada hora do dia, podemos tratar o Sol como fonte pontual, pegando apenas um RL para projetá-la.
Já diferenciamos os tipos de fontes. Agora vamos falar dos tipos de meios por onde os RL se propagam: transparentes, translúcidos ou opacos. As definições são bem simples. Meios transparentes são meios em que a luz se propaga de modo regular, possibilitando a formação de imagens nítidas dos objetos que estão nesse meio. O melhor exemplo seria o vácuo, mas podemos considerar o ar também como um meio transparente. Até mesmo um vidro perfeitamente polido pode ser considerado transparente. Já em meios translúcidos os RL apresentam uma propagação difusa, sofrendo desvios ao longo do trajeto, dificultando a visualização dos objetos. E nos meios opacos os RL não conseguem se propagar. Quando uma luz é incidida sobre uma parede, por exemplo, não conseguimos ver o que está além dela porque parte da luz é absorvida e parte refletida, não deixando nenhuma parte ser transmitida. O interessante é que a parede é opaca à luz, mas permite que ondas sonoras a atravessem, assim como algumas ondas eletromagnéticas de menor frequência que a luz, como ondas de rádio e wi-fi (elas difratam pela parede, como vimos no módulo de ondas).
Sabemos os tipos de fontes e de meios onde os RL se propagam (ou não, no caso de meios opacos). Vamos estudar as propriedades dos RL agora.
PRINCÍPIOS DOS RAIOS LUMINOSOS
RETILINEARIDADE
Os RL se propagam em linhas retas.
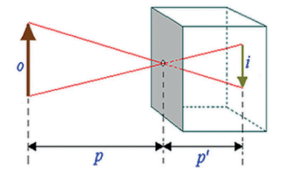
Exemplo: câmara escura.
REVERSIBILIDADE
INDEPENDÊNCIA
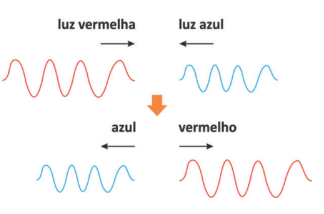
Duas ondas podem sofrer interferência, porém, após a interferência, os feixes continuam como antes.
Exemplo: não confunda luz com tinta. Não há mistura (não veremos uma luz roxa nesse caso).
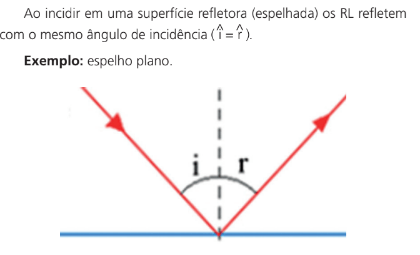
ESPELHO PLANO
Vamos utilizar as duas primeiras propriedades para estudarmos formação de imagens em espelhos planos. Veja a figura abaixo:
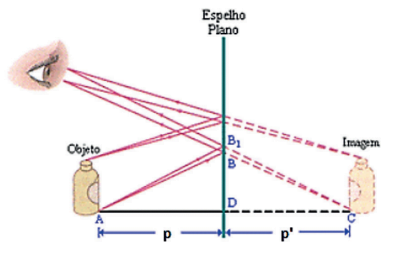
Vamos aos pontos importantes que podemos notar a partir da figura acima:
• a distância do objeto até o espelho (p) é a mesma da imagem ao espelho (p’);
• a imagem formada tem o mesmo tamanho que o objeto (o = i), é direita (não é invertida) e é formada através de prolongamento dos RL (eles não atravessam o espelho, então tomamos a direção do raio incidente e a prolongamos para ver a posição da imagem). Note também que a imagem está rotacionada em relação ao eixo do espelho. Dizemos que a imagem formada é enantiomorfa (ao levantar a sua mão direita em frente a um espelho, por exemplo, irá observar que na sua imagem é a mão esquerda que aparece levantada).
Sempre que quisermos classificar uma imagem, teremos que usar três adjetivos. A imagem formada, de modo geral, seja em um espelho plano, esférico ou em lentes, pode ser:

Como podemos classificar uma imagem formada por um espelho plano? É simples. Não importa a distância que o objeto esteja do espelho, a imagem sempre será: virtual, direita e igual. O que nos leva a uma questão muito importante: imagina que uma pessoa de 1,80m esteja diante de um espelho plano de 80 cm e ela quer se ver por inteira no espelho. O que ela deve fazer? Se a sua resposta foi se afastar do espelho, você, como a imensa maioria, estão errados. Como vimos, a imagem formada não diminui à medida que você se afasta. Conclusão: não importa o que você faça, nunca conseguirá. Para se observar por inteiro o espelho deve ter, no mínimo, a metade da sua altura, conforme mostra a figura.
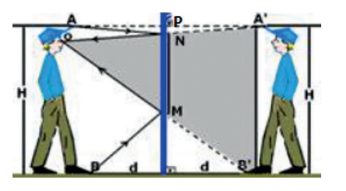
Note as relações de semelhanças:
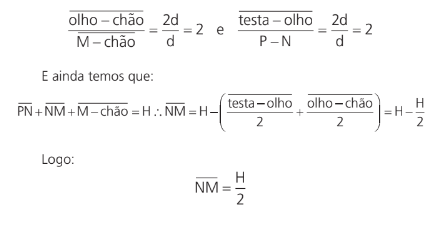
Porém, dependendo do tamanho do espelho e da sua distância até um observador, ele poderá ver a imagem formada por alguns objetos que estão atrás do observador. Veja a figura abaixo:
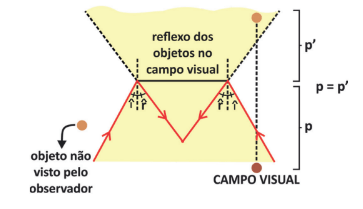
Nesse caso, o observador O consegue ver toda a região marcada. Qualquer objeto ali terá a sua imagem formada atrás do espelho e poderá ser vista pelo observador. Chamamos essa região de campo visual.
TRANSLAÇÃO DE ESPELHOS PLANOS
Vamos comparar as duas figuras abaixo:
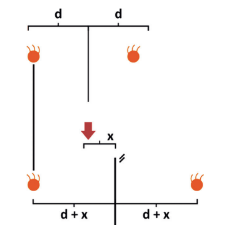
Note que a distância entre o objeto e a imagem antes era 2d e, após arrastar o espelho de uma distância x, a nova distância entre o objeto e a imagem será 2d + 2x. Ou seja, em relação a um observador em repouso, a velocidade da imagem é o dobro da velocidade do espelho.
Mas e se o observador estiver se movendo em relação ao solo?
Bom, nesse caso, como sabemos que a velocidade da imagem em relação ao solo é o dobro da velocidade do espelho, teremos que:

Usando os nossos conhecimentos de referenciais e movimento relativo, sabemos que o sinal de + será usado quando a velocidade do observador tem sentido oposto a do espelho e, o de -, quando estiverem no mesmo sentido.
ROTAÇÃO DE ESPELHOS
Vamos comparar as duas figuras abaixo:
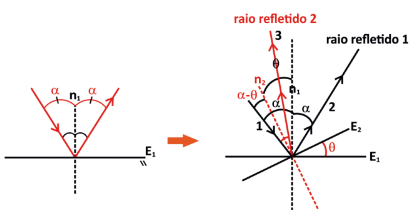
Antes o ângulo entre o raio incidente e o refletido era 2α. Após rotacionar o espelho de θ, o ângulo entre os raios incidente e refletido passa a ser 2(α–θ). Ou seja, quando o espelho sofre uma rotação de um ângulo θ, o raio refletido sofrerá um desvio de 2θ. Logo, a velocidade angular da imagem, para um observador em repouso, será o dobro da velocidade angular de um espelho submetido a uma rotação de frequência constante.
NÚMERO DE IMAGENS FORMADAS POR DOIS ESPELHOS JUSTAPOSTOS FORMANDO UM ÂNGULO θ ENTRE SI
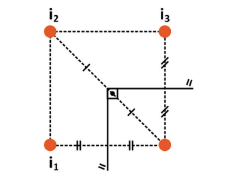
Usando um transferidor na base, e colocando um objeto na bissetriz do ângulo θ formado entre os espelhos, poderemos ver que, quando θ = 30°, teremos 11 imagens. Mudando o ângulo para 45°, teremos 7 imagens e 60°, por exemplo, serão formadas 5 imagens. Conseguimos, empiricamente, através dessas observações, chegar à seguinte relação:
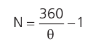
Em que N é o número de imagens formadas por dois espelhos quando um objeto é colocado na bissetriz do ângulo θ entre os espelhos. Se 360/θ for ímpar, o objeto deve estar na bissetriz. Se for par, pode estar em qualquer lugar no setor, inclusive na bissetriz.
Observação
O número de imagens deve ser natural, logo, não funciona para qualquer ângulo.
ESPELHOS ESFÉRICOS (USANDO APROXIMAÇÃO DE GAUSS)
Existem dois tipos de espelhos esféricos: côncavos e convexos. O que os diferencia é que o primeiro tem a parte espelhada voltada para dentro enquanto o convexo tem a parte espelhada para fora, conforme as figuras abaixo:
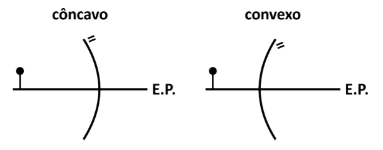
Algumas nomenclaturas são importantes para o nosso estudo:
Eixo Principal (E.P.): é a reta horizontal traçada nas figuras acima. Divide o espelho em duas metades.
Vértice (V): é o ponto do espelho que toca o E.P.
Centro (C): se completarmos mentalmente o espelho até formarmos uma esfera, podemos perceber que o ponto C nas figuras acima representa o centro geométrico dessa esfera formada. Sendo assim, a distância do ponto C ao vértice é equivalente ao raio do espelho esférico.
Foco (F): perceba, pelas figuras, que os RL que são paralelos ao E.P., após refletirem no espelho, tocam o E.P. em um ponto. Esse ponto é o foco do espelho. Se pegarmos infinitos RL paralelos ao E.P.,
o mesmo aconteceria com todos eles. Todo raio que se aproxima do espelho paralelamente ao E.P., será refletido e passará pelo foco.
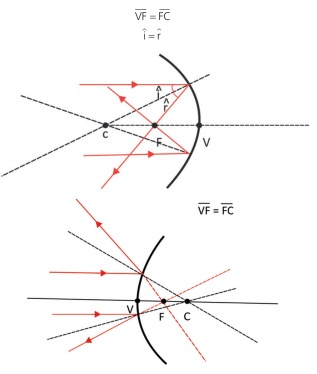
Observação
A geometria nos diz também que toda reta que passa no centro e toca na superfície da esfera é uma reta normal à reta tangente à esfera nesse ponto. Sendo assim, imaginando que estamos falando de uma superfície espelhada, o ângulo de incidência é zero e, portanto, o de reflexão também será zero. Ou seja, todo R.L. que passa pelo centro, após ser refletido pelo espelho, voltará pelo centro.
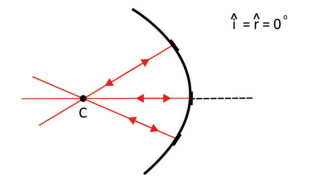
Agora nós sabemos exatamente o que acontece com os R.L. quando se aproximam de um espelho esférico, ou passando pelo centro, ou se propagando paralelamente ao E.P. Sabendo isso, podemos prever onde esses raios se encontrarão, formando a imagem do objeto.
Começaremos pelo côncavo. Esse espelho, diferentemente do plano, forma imagens diferentes dependendo da distância do objeto até o espelho. São cinco imagens com características diferentes. Cada uma representada abaixo:
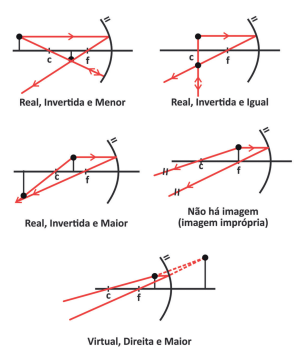
Através das figuras acima, no caso do espelho côncavo, podemos ver que se o objeto estiver:
• antes do centro, a imagem será real, invertida e menor;
• no centro, a imagem será real, invertida e igual;
• entre o centro e o foco, a imagem será real, invertida e maior;
• no foco, não haverá imagem;
• entre o foco e o vértice, a imagem será virtual, direita e maior.
Já no espelho convexo, a formação da imagem é bem mais simples.
Só há uma possibilidade, não importando a posição do objeto:
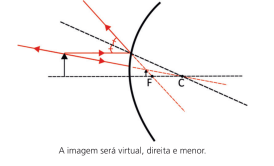
Observação
Na figura abaixo, temos uma fonte distante. Perceba como se dá a reflexão no caso dos espelhos esféricos. O importante é analisarmos, em especial, o que ocorre no espelho convexo. Perceba que esse tipo de espelho proporciona um grande campo visual e, por causa disso, é usado em ônibus, portarias de prédios, nos automóveis etc.
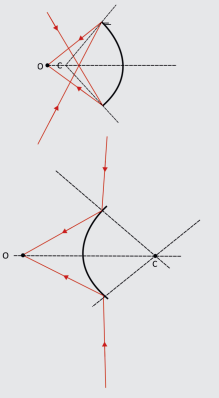
RELAÇÕES MÉTRICAS NOS ESPELHOS ESFÉRICOS
Vamos chamar a distância do objeto ao espelho de p e a distância m da imagem ao espelho de p’. As relações métricas importantes para os nossos estudos são:
EQUAÇÃO DO FOCO (COM APROXIMAÇÃO DE GAUSS)
Não dedicaremos espaço aqui para a dedução da equação. Caso seja de interesse do leitor, procure o livro Curso de Física Básica – Volume IV, do professor Moysés. Lá encontrará muito mais que as deduções das equações.
Veja as figuras abaixo:
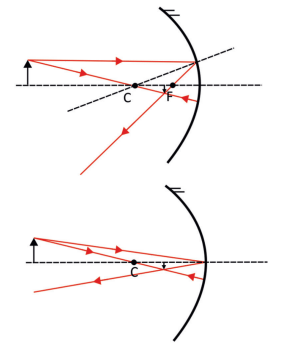
Parecem que são duas figuras diferentes, mas na verdade usam o mesmo princípio. Na 1a figura, um RL está em cima da reta normal (reta que passa pelo centro, conforme vimos na Observação). Já na 2a figura, pegamos outro RL cujo ângulo com a normal (que, nesse caso, é o EP – note que o EP é também normal, já que passa pelo centro) vale α. Sendo assim, seguindo o princípio da reflexão, o ângulo refletido também será α, formando a mesma imagem da figura anterior.
Na verdade, os dois métodos se equivalem porque estamos usando a aproximação de Gauss. Essa aproximação leva em conta um baixo ângulo de abertura θ, de modo que poderemos fazer senθ ≈ tanθ ≈ θ, medido em radianos. A mesma aproximação valerá para os outros ângulos destacados. Usando essas aproximações acima, lei dos senos e um pouco de geometria, conseguiremos chegar à equação do foco de Gauss:
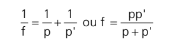
Lembrando que p é a distância do objeto ao espelho e p’ a distância da imagem ao espelho.
Com a mesma matemática, é possível encontrarmos a relação abaixo também:
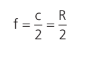
A distância do espelho ao foco é a metade da distância do espelho ao centro, que representa o raio do espelho esférico. Perceba também que, usando semelhança de triângulos, conseguimos chegar a mais uma importante relação:
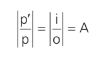
Em que A é o aumento linear (tamanho da imagem em relação ao do objeto). Se 0 < A < 1, a imagem é menor que o objeto.
Observação
Importante percebermos que a relação acima é puramente geométrica. Trata-se apenas de distâncias, m logo, valores positivos. É muito comum usarmos a equação acima para encontrarmos p ou p’ e substituirmos na equação de Gauss, para descobrir o foco do espelho. Antes de substituir, veja se há a necessidade de trocar o sinal de p’, por exemplo. Um erro em algum sinal pode ser fatal nesse tipo de problema. Para entender melhor, veja o exemplo abaixo, assim como a tabela dos sinais.
Exercício Resolvido
01. Um objeto encontra-se na frente de um espelho esférico de raio 12 cm. A imagem formada é direita e tem apenas 60% do tamanho do objeto. Qual a distância do objeto ao espelho?
Resolução:
Se a imagem é menor que o objeto e é direita, sabemos que se trata de um espelho convexo e que a imagem é virtual, direita e menor (o espelho côncavo não produz imagem direita e menor).
Aí fica o alerta → Se a imagem é virtual, p’ é negativo (a imagem se forma atrás do espelho – sendo assim, pensando em eixos, p’ estaria na parte negativa) e, sendo um espelho convexo, a sua parte espelhada fica para fora, então o foco aparece também atrás do espelho → espelho convexo tem foco negativo. Nesse caso, -6 cm (lembre-se que o foco é a metade do raio). Aplicando a relação de semelhança:
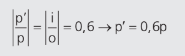
Se usássemos essa relação na equação de Gauss, erraríamos o problema. A relação acima é geométrica. Corrigindo o sinal (porque temos uma imagem virtual), p’ = –0,6p. Agora sim, substituindo na equação de Gauss:
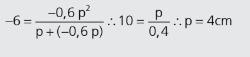
Observação
Fique sempre atento aos sinais. Tanto do p’ quanto do f.
TABELA DOS SINAIS

REFRAÇÃO DA LUZ
É quando uma onda sofre uma mudança na sua velocidade devido à mudança do meio de propagação. A velocidade da luz no vácuo é 3 · 108 m/s, já a velocidade da luz na água é na ordem de 2,2 · 108 m/s.
No módulo de ondulatória, esse fenômeno é abordado de uma maneira mais detalhada. Por hora, o mais importante é entendermos que essa mudança na velocidade da luz pode causar um desvio do RL (falamos de ângulo de incidência ser diferente do ângulo de refração, o ângulo entre o RL e a normal após mudança de meio de propagação).
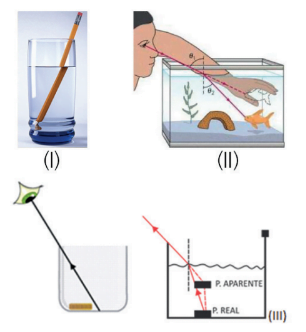
Na figura I, a refração faz com que o lápis aparente estar quebrado. Vamos analisar com mais detalhes o que acontece na figura II. A imagem formada do peixe para o menino está exatamente onde a sua mão se encontra, porém, como o RL sofre refração, o peixe está, na verdade, um pouco abaixo. É por isso que objetos no fundo de um copo com água aparentam estar um pouco acima de onde realmente estão. O mesmo vale para a profundidade de uma piscina. A distância entre a superfície de separação entre os meios e a posição onde a imagem se forma é chamada de altura aparente. A distância até onde o objeto de fato está é chamada de altura real.
Na figura III, antes de colocar água no copo, o observador não conseguia ver o objeto. Colocando água lentamente, o objeto passa a ser, aos poucos, visível. Note que, com o nível de água da figura, o observador verá a metade direita do objeto.
Abaixo temos, à esquerda, uma onda sonora (mecânica) e, à direita, um raio luminoso (onda eletromagnética), sofrendo refração ao sair do ar e entrar na água:
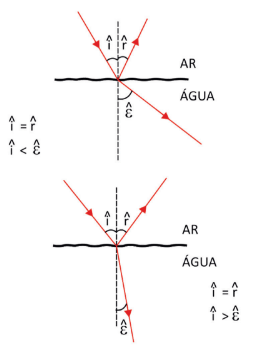
Perceba que, no primeiro caso, o vetor que indica a direção de propagação da onda se afasta da normal. Isso acontece porque o som é mais rápido na água que no ar.
Já na segunda figura, o ângulo entre a direção de propagação e a normal diminui, já que a luz perde velocidade ao entrar na água.
Agora olhe o que acontece com os comprimentos de onda durante a refração:
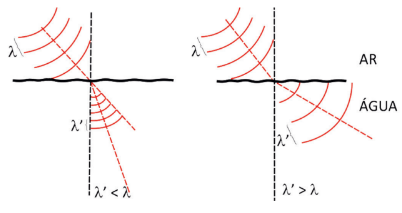
A frequência da onda não é alterada com a mudança de meio (uma luz vermelha não vai virar azul porque entrou na água, por exemplo). O comprimento de onda muda devido à mudança de velocidade. Sendo assim:
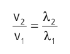
No caso específico da luz, dizemos que quanto maior o índice de refração do meio (n), menor será a sua velocidade de propagação.
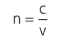
Em que c é a velocidade da luz no vácuo e v a velocidade da luz no meio. Sendo assim, podemos comparar as velocidades de propagações nos meios através dos seus índices de refração:
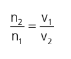

Essa é a lei de Snell. A sua dedução também pode ser encontrada no livro citado anteriormente do Moysés.
Sempre que um RL atinge uma superfície haverá refração? Não. Aí é que está o detalhe. Se o RL atingir uma superfície com maior índice de refração, haverá, além da reflexão, refração. Porém, se o RL vier de um meio mais refringente e atingir a superfície de um meio menos refringente, pode ou não haver refração, mas haverá sempre reflexão. Se não houver refração, dizemos que haverá reflexão total. Mas qual seria então essa condição? Como saber se haverá refração e reflexão ou só reflexão (reflexão total)?
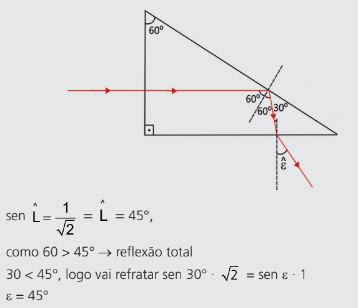
Observe a figura a seguir:
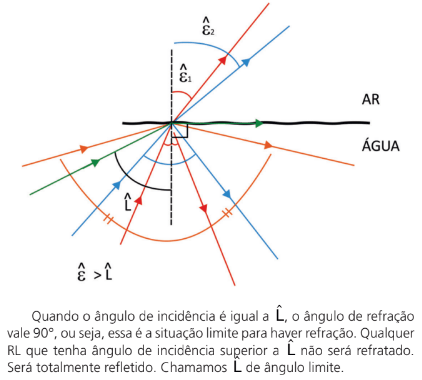

Exercício Resolvido
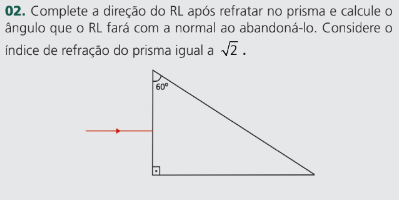
Resolução:
LENTES DELGADAS
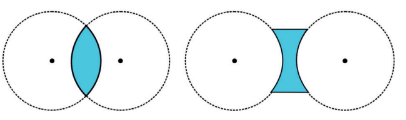
Visto isso, vamos estudar lentes. São instrumentos ópticos que, assim como os espelhos esféricos, produzem diferentes imagens, dependendo da posição do objeto. Existem dois tipos de lentes, as de bordo no e as de bordo grosso.
Para descobrirmos o caminho do RL (e assim o caráter da lente, convergente/divergente), temos que saber a relação entre o seu índice de refração e o índice do meio. Abaixo temos uma lente (biconvexa) cujo índice de refração é maior que o meio:
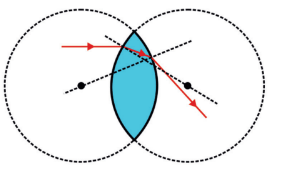
Não é necessário fazer os círculos para sabermos o caminho do RL. Veja as duas figuras abaixo:
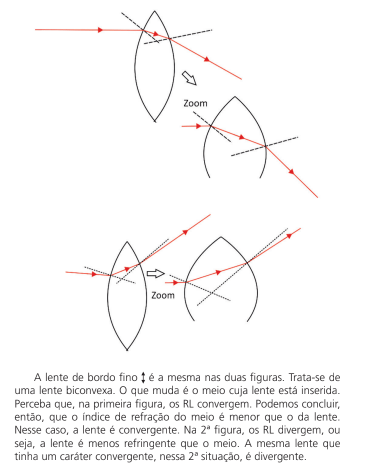
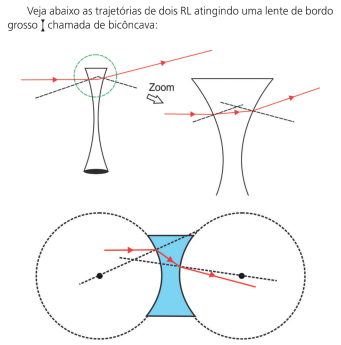
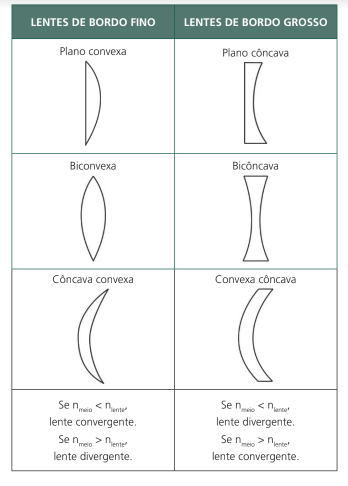
Veja que, nesse caso, quando a lente é mais refringente que o meio, ela será divergente e, se a lente for menos refringente que o meio, será convergente. Abaixo há um esquema com os tipos de lentes e as suas características:
Observação
Geralmente, a lente está imersa no ar, ou seja, o seu índice de refração é maior que o do meio. Logo, a lente de bordo no será convergente e a de bordo grosso, divergente.
E como é formada a imagem em uma lente? Vamos considerar que as lentes estão imersas no ar. Sendo assim, as figuras abaixo fazem referência às imagens formadas por uma lente convergente:
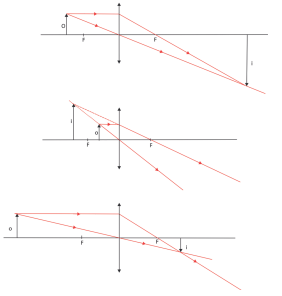
Veja que as classificações das imagens dependem da distância do objeto em relação à lente convergente e se dá de maneira semelhante às imagens formadas por um espelho côncavo.
Já a lente divergente, como podemos ver abaixo, só forma um tipo de imagem, assim como o espelho convexo:
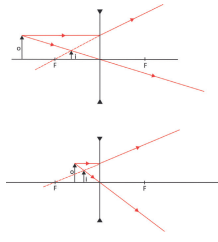
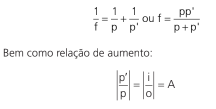
As semelhanças com os espelhos esféricos continuam quando queremos achar a distância da imagem em relação à lente p’, por exemplo:
Observação
Devemos manter a atenção aos sinais. Imagem virtual, p’ negativo. O mesmo cuidado deve ser mantido. Em relação ao sinal dos focos, aqui, a lente convergente terá f > 0 e a lente divergente, f < 0.
O que muda é, dados os raios das lentes e o seu índice de refração, como encontramos o seu foco (aqui, a relação f = R/2 não faz sentido algum). Uma lente plano-convexa (uma lupa, por exemplo) pode ter o raio da parte convexa igual a 10 cm (o raio da parte plana, por ser uma superfície plana, tende ao infinito). Vamos escolher o seu índice de refração igual a 2. Qual será o foco dessa lente?
Para encontrarmos, temos que usar a equação dos fabricantes de lente, ou equação de Halley:

Observação
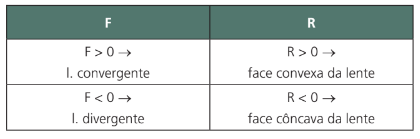
Novamente atenção aos sinais. Se a face da curvatura for convexa, R > 0. Se for côncava, R < 0.
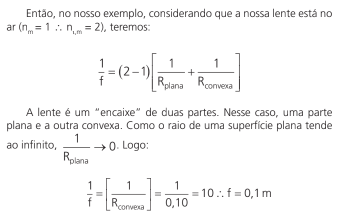
Perceba que utilizamos o raio em metros, sempre.
Se um objeto estiver a no máximo 10 cm da lente, sua imagem será virtual, direita e maior. Quanto mais próximo do foco, maior a imagem será. Se o objeto estiver a 8 cm da lente, por exemplo, o aumento proporcionado por essa nossa lupa será de:
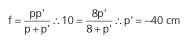
O sinal negativo aparece devido ao fato de a imagem ser virtual.
Então:
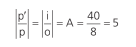
A imagem será 5x maior que o objeto.
Vamos a mais um exemplo:
Exercício Resolvido

Resolução:
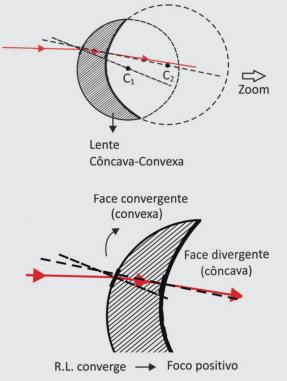
Lembrando-se de como é o formato de uma lente côncava-convexa, podemos ver que a parte côncava tem um raio de curvatura maior que a parte convexa. Após passar pela primeira face, o R.L. se aproxima da normal, mostrando o caráter convergente da face. Já na segunda face, o R.L. se afasta da normal, mostrando o caráter divergente da face. Sendo assim, 20 cm é o raio da parte convexa e 25 cm, o da parte côncava (teremos que trocar o seu sinal).
Usando a equação de Halley:
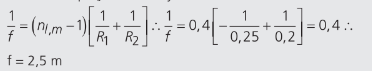
Agora que sabemos o seu foco, vamos voltar à equação de Gauss:
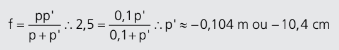
O sinal negativo é porque a trata-se de uma imagem virtual. Sendo assim, o aumento linear será:
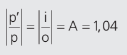
Um aumento de apenas 4%.
Tabela de Sinais
INSTRUMENTOS ÓPTICOS
São instrumentos usados para nos auxiliar na visualização de objetos ou por serem muito pequenos – microscópios, lupas – ou por estarem muito longe – telescópios, lunetas, binóculos. Óculos (de grau), projetores e câmeras fotográficas também são exemplos de instrumentos ópticos. Vamos estudar problemas visuais logo após essa etapa. Por hora, vamos discutir alguns dos instrumentos acima.
LUPA
A lupa é formada por uma lente convergente, ou seja, nem sempre ela irá formar uma imagem ampliada do objeto. Como vimos anteriormente, a imagem será ampliada (virtual, direita e maior) apenas se o objeto estiver entre a lente e o seu foco e, quanto mais próximo do foco, maior será a ampliação.
Entendemos, então, que o objeto deve estar próximo da lupa. Agora, onde será formada a imagem? Essa etapa é importante. Para enxergarmos com nitidez, a imagem deve ser formada dentro do nosso olho, na retina. Significa que devemos estar a uma distância mínima do objeto para vê-lo. Nos aproximando mais que isso, a imagem não se formará na retina, ficando “fora de foco”, sem nitidez.
A distância mínima que um objeto deve estar do olho é de 25 cm, para ser visto com nitidez (imagem formada na retina).
Na figura abaixo, podemos ver a trajetória dos RL ao utilizarmos uma lupa:
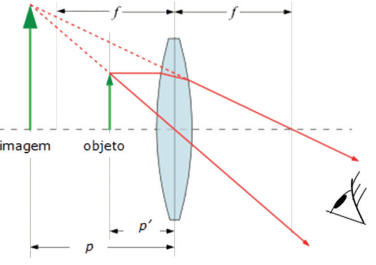
O objeto encontra-se antes do foco, proporcionando uma imagem virtual, direita e maior. Agora, vamos comparar como vemos o objeto sem a lupa e como vemos com a lupa, a m de encontrarmos o aumento proporcionado pela lente.
Sem a lupa:
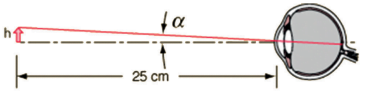
Com a lupa:
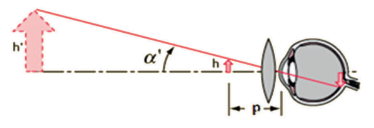
Sendo assim:

Porém, apesar dessa ampliação que a lupa proporciona, não é o suficiente para enxergarmos objetos microscópicos. Para isso, é necessário fazer, por exemplo, uma associação de duas lentes convergentes, que ficam a certa distância uma da outra. A mais próxima do olho é chamada de lente ocular e a mais próxima do objeto, lente objetiva. Com essas duas lentes podemos montar um microscópio composto.
MICROSCÓPIO COMPOSTO
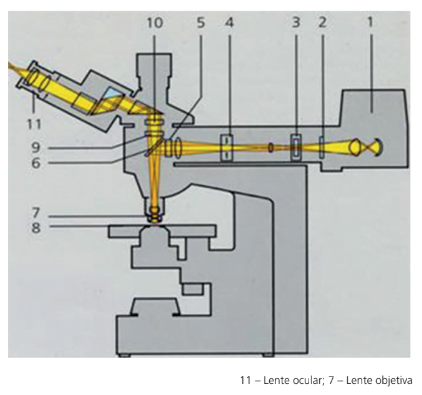
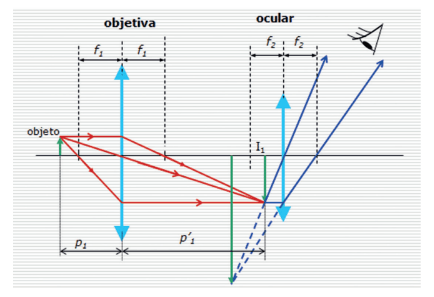
A figura anterior mostra o comportamento do RL, desde o objeto até o olho do observador, passando pelas lentes convergentes objetiva e ocular. Para descobrir a sua ampliação total (que pode ser superior a 1000x), temos que aplicar a equação de Gauss na lente objetiva, descobrindo a distância da imagem até a lente. Sabendo a distância do objeto à lente, podemos descobrir o aumento que essa lente proporciona. Após fazermos o mesmo raciocínio para a lente ocular.
Ao final, multiplicando os dois aumentos, conseguiremos o aumento total (por exemplo, se a 1a lente aumentar 20x e a 2a, 5x, teremos um aumento total de 100x).

TELESCÓPIO REFRATOR
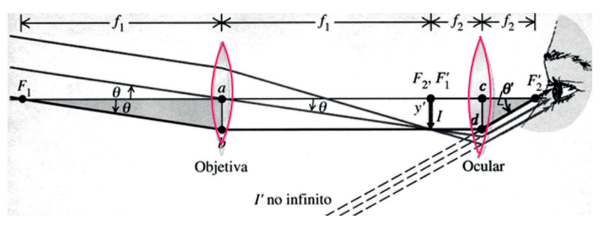
Nesse caso, o objeto observado está no infinito. Sendo assim, fica fácil ver, pela equação de Gauss, que a imagem formada pela lente objetiva ficará no seu foco. Essa imagem será objeto da próxima lente, a ocular, que funcionará como uma lupa. Ou seja, a luneta é montada de forma que a imagem formada pela 1a lente que muito próxima ao foco da 2a lente, proporcionando, assim, um grande aumento:
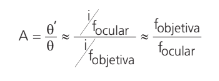
UM POUCO MAIS SOBRE O OLHO HUMANO E CORREÇÕES DE ALGUNS PROBLEMAS VISUAIS
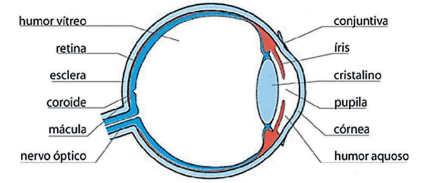
O olho humano tem aproximadamente 2,5 cm e consegue formar imagens (na retina) de objetos próximos (distância mínima de 25 cm, chamada de ponto próximo) e distantes. Para isso, o olho ajusta o seu foco.
Na figura abaixo temos, à esquerda, o ajuste para objetos distantes e, à direita, o ajuste para objetos próximos. Essa estrutura biconvexa é o cristalino. Por ser elástico, consegue contrair e relaxar, se ajustando a cada situação.
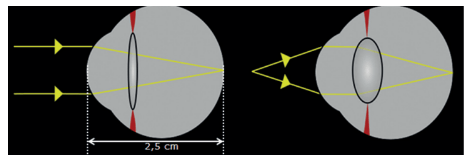
Essa distância focal pode mudar dentro de um limite curto, conforme mostra a tabela abaixo:
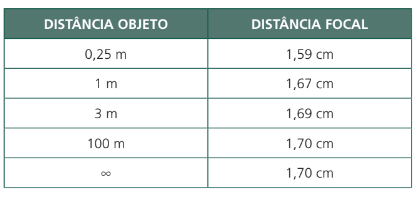
Por exemplo, para um objeto no ponto próximo, temos que:
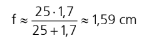
Considerando que a distância entre a imagem e a lente, ou seja, entre a retina e o cristalino é de aproximadamente 1,7 cm. Alguns exercícios consideram 1,5 cm e o tamanho do olho 2,0 cm.
Conforme envelhecemos, o cristalino perde elasticidade, tornando esse processo de acomodação visual gradativamente mais difícil, surgindo um problema visual chamado de presbiopia (popularmente conhecido como vista cansada). A pessoa começa a apresentar dificuldades para enxergar objetos próximos. Para corrigir esse problema é necessário usar lentes convergentes.
Além desse problema, pode ser que o cristalino perca a sua transparência. A pessoa passará a ter uma visão borrada. Esse problema de visão é chamado de catarata e, para corrigi-lo, deve-se substituir o cristalino por uma lente convergente artificial. Outra complicação que pode estar associada ao cristalino é o astigmatismo. A imagem formada na retina não é nítida devido ao formato irregular ou do cristalino ou da córnea (formato mais ovalado). Para corrigir esse problema, a pessoa deve usar lentes divergentes cilíndricas (ou tóricas).
Os outros problemas de visão que estudaremos não estão associados ao cristalino (na verdade podem estar relacionados ao seu formato, mas não será a causa principal para os nossos estudos), mas sim ao fato de a imagem não se formar na retina, ou seja, não formar uma imagem nítida. Isso pode acontecer ou porque o globo ocular é maior que o padrão, fazendo com que a imagem se forme antes da retina ou porque o globo ocular é menor, fazendo com que a imagem se forme após a retina.
Vamos começar pela primeira situação:
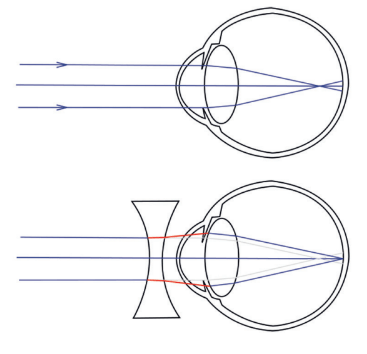
Pela figura acima, perceba que antes a imagem se formava antes da retina e, após o uso de lente divergente, a visão da pessoa passa a ser corrigida. Esse problema de visão é a miopia.
Vamos agora para a segunda situação:
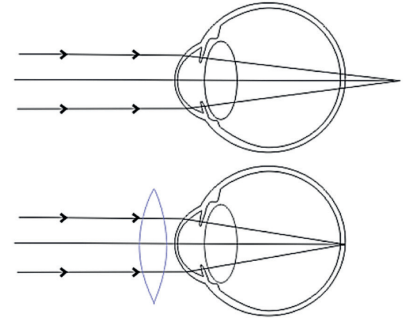
Pela figura acima, perceba que antes a imagem se formava após a retina e, após o uso de lente convergente, a visão da pessoa passa a ser corrigida. Esse problema de visão é a hipermiopia.
UM POUCO MAIS SOBRE REFRAÇÃO

Vimos anteriormente, nos nossos estudos de refração, que a frequência de uma onda não se altera quando o meio de propagação é alterado, mas o que deve acontecer com uma luz que não é monocromática, ou seja, uma luz com mais de uma frequência (cor), como a luz solar, por exemplo, quando muda de meio?
Esse fenômeno é conhecido como dispersão luminosa. A luz solar (luz branca), quando se propaga do ar para água, sofre dispersão, que nada mais é que a separação das luzes que a compõem, que são várias, mas podemos falar em 7 principais: Vermelho, Alaranjado, Amarelo, Verde, Azul, Anil e Violeta – VAAVAAV – sendo o vermelho a cor de menor frequência (portanto, maior comprimento de onda) e o violeta, a cor com maior frequência (menor comprimento de onda).
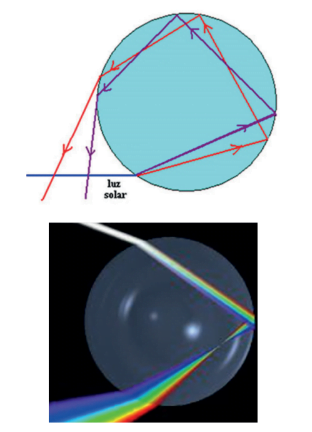
A dispersão foi observada por Newton, em 1666, quando deixou a luz do Sol incidir em um prisma. Seu estudo foi publicado no seu livro de tratado da óptica.
No vácuo, uma luz monocromática vermelha possui a mesma velocidade que uma violeta, por exemplo. Não importa a cor (frequência). A velocidade de qualquer luz (na verdade de qualquer onda eletromagnética, como o rádio, raio-X etc) no vácuo é igual a c (3.108 m/s). Porém, em outro meio, como a água, a velocidade de cada frequência é diferente e é justamente isso que faz a dispersão acontecer.
Veja a figura abaixo. Um feixe de luz branca está indo do ar para água. Na dispersão, a luz com maior velocidade (vermelho) se afasta da normal, obedecendo ao princípio da refração e, a mais lenta (violeta), será mais próxima da normal.
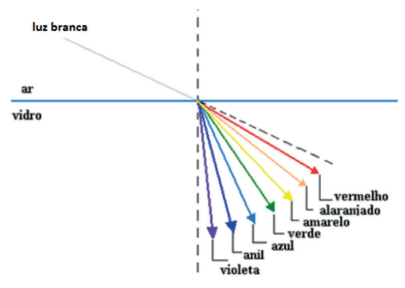
Um prisma funciona como a água nesse caso, fazendo a luz sofrer dispersão:
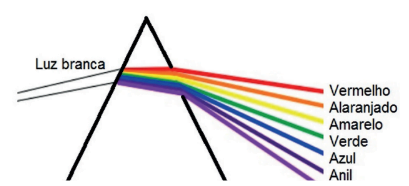
Mas e se a luz branca estiver saindo da água (ou de um prisma) e indo para o ar?
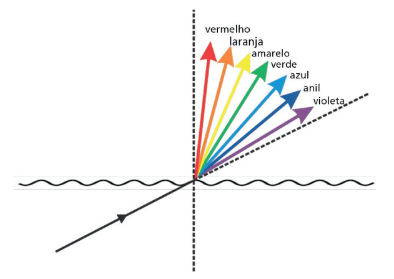
Note pela figura acima que, pela equação de Snell, temos uma inversão em relação à dispersão ar – água. Nesse caso, o vermelho tende a se aproximar mais da normal que o violeta.
Com isso, conseguimos entender um dos fenômenos mais belos da natureza, o arco-íris. As gotículas de água em suspensão no ar funcionam como pequenos prismas. A luz do Sol, ao penetrar nessas gotículas, sofre dispersão, como podemos ver com mais detalhes na figura abaixo: