POLINÔMIO

MONÔMIO
É o polinômio que possui um único termo.
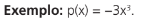
POLINÔMIO COMPLETO
É aquele que não possui coeficientes nulos. Um polinômio completo de grau n possui n + 1 termos.
VALOR NUMÉRICO
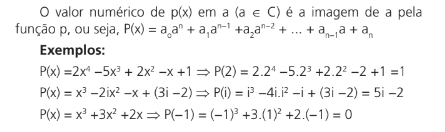
Observação

RAÍZES

GRAU
Dado um polinômio P(x) com pelo menos um termo de coeficiente não nulo, o grau de P, indicado por gr(P) é o maior dos expoentes da variável x nos termos com coeficientes não nulos.
Se P tem todos os coeficientes nulos, não se define o grau de P.
Exemplo:
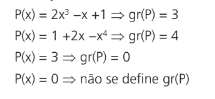
OPERAÇÕES COM POLINÔMIOS
ADIÇÃO E SUBTRAÇÃO DE POLINÔMIOS:
A adição e a subtração de polinômios são feitas somando-se ou subtraindo-se os coe cientes dos termos de mesmo grau em todas as variáveis.
Exemplos:
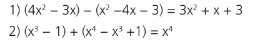
Atenção!
Frequentemente na subtração de polinômios é preciso eliminar parênteses. Deve-se atentar para o fato do sinal menos incidir sobre todos os termos entre parênteses de acordo com a propriedade distributiva da multiplicação.
Exemplo:
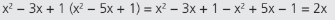
MULTIPLICAÇÃO DE POLINÔMIOS
Para multiplicar polinômios basta aplicar a distributividade da multiplicação.
Exemplo:
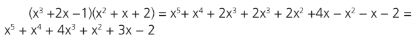
Note que se o produto de dois polinômios é nulo, pelo menos um dos polinômios deve ser nulo.
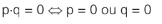
Observação

DIVISÃO DE POLINÔMIOS
Dados dois polinômios P(x) e D(x), de graus p e q, respectivamente, dividir P(x) por D(x) significa é encontrar dois polinômios Q(x) e R(x), denominados quociente e resto, respectivamente, que satisfazem


Exemplo:

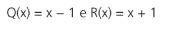
Observação

IDENTIDADE DE POLINÔMIOS
Dois polinômios são ditos idênticos quando têm sempre o mesmo valor qualquer que seja o valor atribuído à variável.
Importante!
Dois polinômios idênticos são sempre de mesmo grau e têm todos os coeficientes iguais.



Polinômio identicamente nulo: É aquele que é nulo para qualquer valor da variável. Um polinômio identicamente nulo tem todos os seus coeficientes iguais a zero.
Observação
Se um polinômio de grau n possuir mais de n raízes, então ele é identicamente nulo.
TEOREMA DE D’ALEMBERT
O resto da divisão de um polinômio P(x) por ax +b, com a ≠ 0, é igual a P(−b/a).
Demonstração:
Na divisão de P(x) por ax +b o resto deve ter grau zero. Assim, podemos dizer que a divisão terá um quociente Q(x) e resto R(x) = R = constante. Logo,

REGRA DE RUFFINI-HORNER
Numa divisão de um polinômio P(x) por x − a, temos:
1º. dispomos a e os coeficientes de P(x) inclusive os nulos
2º. o coeficiente do primeiro termo do quociente é igual ao coeficiente do primeiro termo do dividendo;
3º. o coeficiente do segundo termo do quociente é igual ao coeficiente do segundo termo do dividendo mais o produto do coeficiente do primeiro termo do quociente pelo segundo termo do binômio tomado com o sinal trocado;
4º. em geral, o coeficiente do termo de ordem p do quociente é igual ao coeficiente do termo da mesma ordem do dividendo, mais o produto do coeficiente do termo antecedente do quociente pelo segundo termo do binômio tomado com o sinal trocado;
5º. finalmente, obtém-se o resto da divisão multiplicando o coeficiente do termo constante do quociente pelo segundo termo do binômio tomado com o sinal trocado e adicionando a esse produto o coeficiente do termo constante do dividendo.
Exemplo:
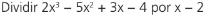
Inicialmente alocar no dispositivo os coeficientes do dividendo e o segundo termo do binômio com o sinal trocado e então proceder como acima:




