MOVIMENTO UNIFORME (M.U.)
O movimento de um móvel depende do referencial. Por exemplo, para o passageiro de um avião, seu assento não está se movendo, ou seja, está em repouso. Para um referencial no solo, (uma pessoa vendo o avião passar) o assento, o passageiro e o avião estão se movendo – e na mesma velocidade. Podemos perceber que o movimento (trajetória e velocidade) de um móvel não possui, então, uma resposta única. Para descrevermos o movimento de um móvel, vamos usar a abscissa como referência, com origem no 0.
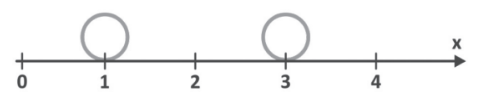
Vamos supor que, no instante inicial, o móvel estava na posição x = 1 m e, após 2 s, foi para a posição x = 3 m. O deslocamento escalar1, ou seja, a variação de posição do móvel, nesse caso, foi de 2 m. Já o intervalo de tempo foi de 2 s.
A velocidade escalar1 média é a razão entre a variação de posição (∆x) e o intervalo de tempo (∆t) gasto pelo móvel durante esse deslocamento. Nesse caso:
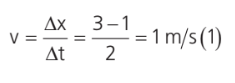
Podemos dizer que a taxa de variação da posição com o tempo foi de 1 m/s. Contudo, apenas com as informações fornecidas não é possível saber se o carro manteve a mesma velocidade durante o seu deslocamento. A velocidade instantânea não é necessariamente igual à velocidade média do móvel. Podemos definir velocidade instantânea como a velocidade que um móvel apresenta em um intervalo de tempo infinitesimal. Por exemplo, ao olharmos para o velocímetro de um carro, por exemplo, é comum vermos a velocidade mudar a cada instante,
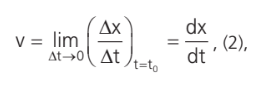
que é a derivada da posição (x) em relação ao tempo (t). Significa dizer que, quanto menor o intervalo de tempo tomado, mais próximo estaremos do resultado exato.
Vamos considerar que nosso móvel, no exemplo acima, manteve a velocidade constante durante o deslocamento. Abrindo a equação (1):
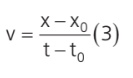
Considerando que o tempo inicial t0 seja zero, temos que:
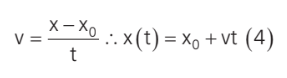
Podemos perceber que a posição do móvel está em função do tempo, e que essa função é linear (uma reta):
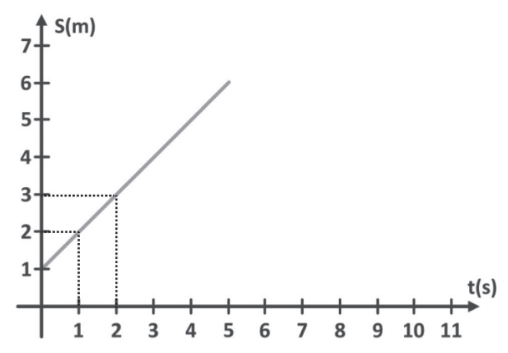
Nesse gráfico, a ordenada representa a posição do móvel, e a abscissa, o tempo.
A posição inicial é 1 m e, a cada segundo, o móvel avança 1 m. Podemos dizer que, numericamente, a velocidade é o coeficiente angular da reta (tangente).
Observação
Se a ordenada, em vez de representar a posição, representar a velocidade, teríamos um gráfico com o seguinte formato:
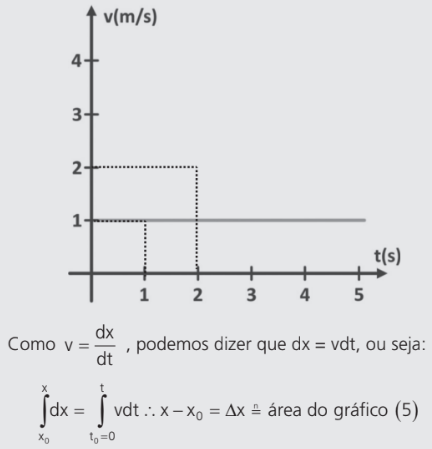
A operação matemática acima se chama integral. Não vamos resolver problemas por integrais e nem precisamos nos preocupar com isso. O importante é sabermos que, de maneira bem simples e superficial, integrar significa somar. Quando realizamos um integral de uma função de um ponto a outro, estamos fazendo a área do gráfico.
ProBizu
Então, quando temos um gráfico v x t, a área será numericamente igual ao deslocamento do móvel. Note que, se considerarmos os dois primeiros segundos, a área valerá 2; o deslocamento do móvel foi exatamente 2 m.
MOVIMENTO RETILÍNEO UNIFORMEMENTE VARIADO (M.R.U.V.)
O que aconteceria se a velocidade do nosso móvel não for constante? Como medimos a sua variação? Essa grandeza está presente no nosso dia a dia. A aceleração escalar média é a razão entre a variação de velocidade (∆v) e o intervalo de tempo em que ocorreu a mudança na velocidade.
Vamos supor que a velocidade inicial do nosso móvel era zero (lembrando que o nosso referencial está centrado na origem, como se fosse um ponto no chão, portanto, a velocidade era zero em relação ao chão) e, após 2s, atingiu 2 m/s. Nesse caso:
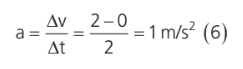
A cada segundo que se passa, a velocidade aumenta 1 m/s (1 m/s a cada s, logo, 1 m/s2). O que aconteceria se a aceleração não fosse a mesma o tempo todo? A aceleração instantânea não é necessariamente igual à aceleração média do móvel. Podemos definir aceleração instantânea como a aceleração que um móvel apresenta em um intervalo de tempo infinitesimal. Se o motorista pressionasse com maior ímpeto o acelerador do carro, a velocidade iria mudar mais rapidamente que no instante anterior.
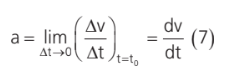
Iremos considerar que o móvel, no exemplo acima, manteve a sua aceleração constante durante o deslocamento. Abrindo a equação (6):
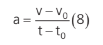
Considerando que o tempo inicial t0 seja zero, temos que:
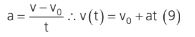
Essa é a equação horária da posição.
Podemos perceber que a velocidade do móvel está em função do tempo, e que essa função é linear (uma reta):
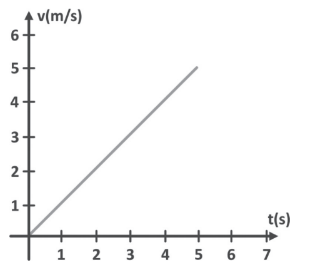
Nesse gráfico, a ordenada representa a velocidade do móvel, e a abscissa, o tempo.
A velocidade inicial é 0 e, a cada segundo, o móvel sofre um aumento de 1 m/s na sua velocidade. Podemos dizer que, numericamente, a aceleração é o coe ciente angular da reta (tangente).
Observação
O gráfico não nos dá informação (diretamente) sobre a posição do móvel. Não nos informa a posição inicial, por exemplo. Mas, como temos um gráfico v x t, se fizermos a área, teremos o deslocamento do móvel. Por exemplo, nos dois primeiros segundos, a área (triângulo) do gráfico é:
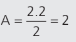
Exatamente o valor do deslocamento do móvel nos 2 s. Não temos como saber a sua posição inicial, mas sabemos que se deslocou 2 m nesses dois primeiros segundos.
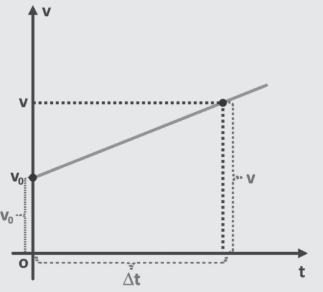
De modo geral, pela área, temos que:
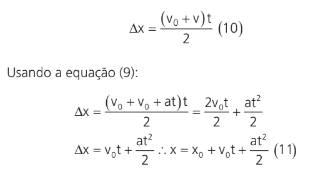
Essa é a equação horária da posição.
Podemos perceber que a posição do móvel está em função do tempo, e que essa função é quadrática (uma parábola). Supondo que a posição inicial seja 1 m e que parte do repouso com aceleração constatante de 1 m/s2, temos o gráfico Xx do movél:
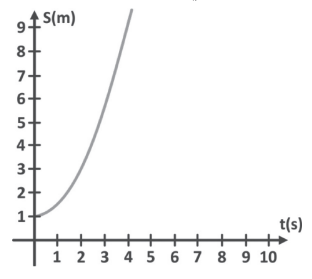
Nossa função, considerando as condições iniciais dadas, é:
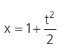
Observação
Se a ordenada, em vez de representar a posição, representar a aceleração, teríamos um gráfico com o seguinte formato:
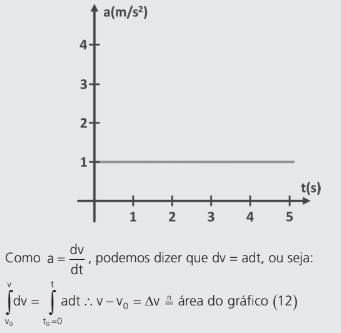
Então, quando temos um gráfico a x t, a área será numericamente igual à variação de velocidade do móvel. Note que, se considerarmos os dois primeiros segundos, a área valerá 2; a variação de velocidade do móvel foi exatamente 2 m/s.
Além das equações (9) e (11), podemos achar uma relação entre velocidades de um móvel após um deslocamento, sem termos conhecimento do intervalo de tempo em que esse evento ocorreu. Vamos substituir a (9) na (11):
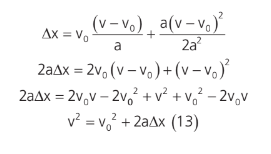
Essa é a equação de Torricelli. As equações (9), (11) e (13) são usadas para medirmos deslocamentos, intervalos de tempo, e velocidades de um móvel em movimento uniformemente variado (M.U.V.) em uma direção. Note que, para a = 0, movimento uniforme (M.U.) em uma direção, as equações se reduzem apenas a equação (4).
CLASSIFICAÇÃO DOS MOVIMENTOS
Quando um móvel apresenta velocidade positiva, ou seja, tem sua variação de posição crescente no tempo, dizemos que está em movimento progressivo. Se sua velocidade for negativa, está em movimento retrógrado ou regressivo.
Por exemplo, quando um carro sai do km 60 para o km 80 em uma rodovia, seu movimento é progressivo. Já os carros que estão no outro sentido da rodovia, do km 80 para o km 60, estão em movimento retrógrado.
Se houver aceleração, e esta aumentar o módulo da velocidade, estará em movimento acelerado. Se o módulo da velocidade estiver diminuindo, o movimento será retardado.
Se, no exemplo anterior, o carro estiver indo do km 60 para o km 80, com sua velocidade aumentando, seria um movimento progressivo e acelerado. Se a sua velocidade estivesse diminuindo, progressivo retardado.
Já os carros que estão se movimentando do km 80 para o km 60, com sua velocidade aumentando, o movimento será retrógrado e acelerado. Se a sua velocidade estivesse diminuindo, retrógrado retardado.
Então:

Exercício Resolvido
01. Vamos analisar o gráfico v x t abaixo:
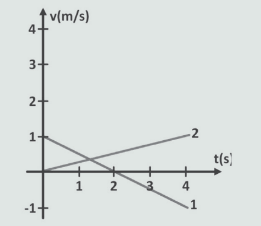
Agora, sabemos que a velocidade inicial do móvel B vale 1 m/s e a sua aceleração é -0,5 m/s2 . Já a velocidade inicial do A é zero e a sua aceleração vale 0,25 m/s2. As acelerações são numericamente iguais às inclinações das retas. Para o 1o, podemos classificar seu movimento como:

SITUAÇÕES PARTICULARES DE MOVIMENTOS UNIDIRECIONAIS
QUEDA LIVRE
Dois objetos quaisquer, de massas diferentes, quando abandonados a certa altura, estão submetidos à mesma aceleração, a gravidade. Então, a taxa de variação de suas velocidades é a mesma, não importando a massa. Esse é o princípio da equivalência, de Galileu Galilei.
Observação
Nossos movimentos não levarão em conta a atuação do ar. Nesse caso, não é a massa que importa, mas o coeficiente aerodinâmico (uma folha de papel amassada ou esticada tem a mesma massa, mas a amassada leva o mesmo tempo para cair, devido a diferenças entre os seus coeficientes aerodinâmicos).
Neil Armstrong largou um martelo e uma pena na superfície lunar, da mesma altura, e chegaram ao solo ao mesmo tempo, comprovando o dito por Galileu.
Vamos imaginar que um objeto foi abandonado a uma altura de 45 m. Quanto tempo leva para tocar no solo? Qual é a sua velocidade nesse instante?
Vamos começar com a equação de Torricelli para descobrirmos a sua velocidade final. Perceba que, como o objeto foi abandonado, v0 = 0, ∆x é o seu deslocamento, ou seja, a altura (h) e a = g = 10 m/s2.

Observação
Conseguimos perceber que o deslocamento no segundo seguinte é 10 m maior que no segundo anterior: 5 m, 15 m, 25 m, 35 m etc. (a, 3a, 5a, 7a etc), essa é a p.a. (progressão aritmética) de Galileu. Por exemplo, no 10º segundo de queda, um objeto percorreria 19.5 = 95 m. Para saber o deslocamento total até o
10º segundo, basta somarmos 5 + 15 + 25 + … + 95 = 500 m. Aplicando-se a equação horária da posição, chegaríamos ao mesmo resultado: ∆x = gt2/2 = 5.102 = 500 m.
LANÇAMENTO VERTICAL
Considere uma situação na qual um objeto é arremessado verticalmente para cima e retorna ao ponto inicial. Vamos analisar primeiro a subida, e depois a descida.
Na subida:

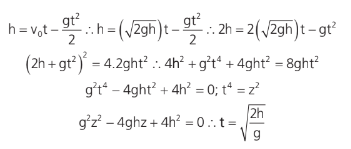
Esse é o tempo que o objeto levaria para alcançar a altura máxima h.
Na descida, a velocidade inicial é zero, então:
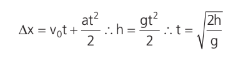
Note que o tempo de descida é igual ao de subida; como a velocidade depende apenas do tempo (mesma aceleração), a velocidade no 1o segundo de subida é igual ao 1o de descida, por exemplo.

Exercício Resolvido
02. Uma bolinha é lançada a partir do solo e retorna após 4,0 s.
a) Qual é a altura máxima?
b) Qual é a velocidade da bolinha no instante final?
c) Qual é a velocidade da bolinha quando t = 1,5 s?
Resolução:




