GRAVITAÇÃO

Podemos observar 5 planetas a olho nu: Mercúrio, Vênus, Júpiter e Saturno (a descoberta de seus anéis foi feita por Newton, que conseguiu, na época, desenvolver um telescópio com ampliação suficiente). Como são observáveis, a existência desses planetas é conhecida desde, praticamente, o início da humanidade.

A origem da palavra “planeta” é grega e significa errante, devido ao fato de as órbitas dos planetas, em relação a um observador na Terra, apresentarem uma trajetória não circular ou elíptica. Em certas épocas, os planetas têm um movimento retrógrado em relação à Terra, ou seja, a trajetória desse planeta parece um laço. Esse movimento é conhecido como movimento errante dos planetas. Mercúrio, por exemplo, apresenta esse movimento 3 vezes por ano. Várias foram as explicações para esses movimentos. Como o céu é um grande laboratório e causa fascínio, muitos estudiosos se dedicaram a tentar explicar o Universo, a sua origem, a nossa posição em relação ao Sol e a outros planetas, o movimento dos planetas, formação etc. Podemos falar de Platão, com a sua ideia de que o Universo deveria ser explicado em termos de formas geométricas perfeitas (círculos e esferas) e de movimentos uniformes, Ptolomeu, com a ideia de que os planetas realizavam órbitas circulares sobre um círculo cujo centro se move com movimento circular sobre um outro círculo, chamado de deferente, com centro na Terra, explicando, assim, o movimento retrógrado dos planetas.

Mas, sem dúvida, um dos grandes nomes da gravitação foi Nikolaus Koppernik (1473-1543), ou Copérnico, como conhecemos. Ele ressurgiu com a ideia do modelo Heliocêntrico, ideia proposta pelos gregos no século III a.C., que havia sido derrubada por alguns motivos, entre esses, a ausência de paralaxe estelar. Se a Terra se movesse em torno do Sol, o ângulo aparente entre as direções de duas estrelas fixas vistas da Terra seria diferente em diferentes épocas do ano, e esse efeito nunca foi observado. O argumento fazia sentido, fazendo com que essa ideia de Heliocentrismo fosse deixada de lado. O erro dessa argumentação é que, as estrelas que observamos parecem estar próximas, mas, na verdade, estão a anos-luz de distância. Tão distantes que o efeito não é observável (só em 1838, com avanço de telescópios).

Copérnico conseguiu, pela 1^a vez, medir as distâncias dos 5 planetas mencionados anteriormente (visto a olho nu) em relação ao Sol. Na verdade, ele criou uma escala relativa. Por exemplo, mediu a distância de Mercúrio até o Sol e encontrou 0,3763 r_T, em que r_T é a distância Terra-Sol. O impressionante é que a medida atual, com todo o avanço tecnológico, é de 0,3871 r_T. Conseguiu também calcular os seus períodos (tempo para dar uma volta no Sol). Sobre Mercúrio, por exemplo, encontrou 87,97 dias, o mesmo valor que conhecemos hoje!

Para entendermos o quão desconfortável era toda essa ruptura no âmbito, não só científico, mas também religioso, em 1600, Giordano Bruno, que havia defendido doutrina de Copérnico, bem como a ideia de que o universo é infinito e que existem várias estrelas parecidas com Sol, foi queimado em Roma, por ordem da Igreja.

Alguns outros estudiosos se basearam nas ideias de Copérnico e deram continuidade aos seus estudos. Em destaque, temos Tycho Brahe e Kepler, o seu assistente. Kepler, após anos de trabalho, percebeu que as trajetórias dos planetas não eram exatamente circulares, como Copérnico propôs, mas levemente ovaladas, com o Sol no eixo, mas não no centro, como também proposto anteriormente. Descobriu que a órbita de Marte era uma elipse, com o Sol em um dos focos, e que o mesmo valia para os outros planetas, obtendo assim a 1^a de suas
três leis:

1^a LEI DE KEPLER OU LEI DAS ÓRBITAS

“As órbitas descritas pelos planetas ao redor do Sol são elipses, com o Sol em um dos focos”.

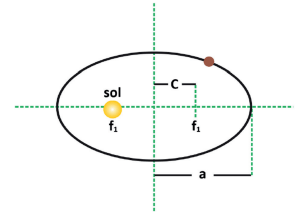
Chamando-se a de semieixo maior e c a semidistância focal, a excentricidade da elipse (e) é e = c/a. Para e = 0, temos um círculo. A excentricidade dos planetas ao redor do Sol é baixíssima. A da Terra, por exemplo, vale 0,017, mostrando o motivo de ter levado muitos a achar que a trajetória era circular. Vênus é o dono da maior excentricidade, 0,206.

Kepler percebeu, também, que o módulo da velocidade dos planetas muda. A velocidade aumenta conforme se aproximam do Sol e diminui conforme vão se afastando, quebrando a ideia de movimento uniforme. Mas, o motivo de isso acontecer, para Kepler, era a atuação de uma força no plano da órbita, tangencial a ela que variasse com o inverso da distância, ou seja, completamente errado (a força é central e varia com o inverso ao quadrado da distância). E, além disso, fez o cálculo errado das áreas varridas pelo raio vetor que liga cada planeta ao Sol. Mas, apesar de todos os erros, conseguiu, com sorte, chegar a um resultado certo.

2^a LEI DE KEPLER OU LEI DAS ÁREAS

“O raio vetor que liga um planeta ao Sol descreve áreas iguais em tempo iguais”.

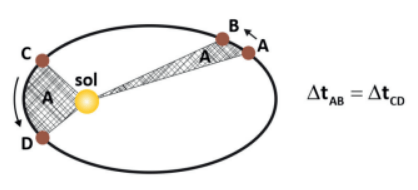
Ou seja, em um mesmo intervalo de tempo, o planeta se deslocaria mais quando estava na região mais próxima em relação ao Sol (periélio) que na região mais afastada (afélio), mostrando que, na região mais próxima a sua velocidade seria maior. Newton, mais tarde, conseguirá explicar de maneira correta a relação acima. Ele conserva uma grandeza física vetorial chamada de momento angular (L), brevemente discutida no módulo de estática (equilíbrio estático de corpos extensos). Essa grandeza está intimamente ligada à outra, de natureza escalar, chamada de momento de inércia (I):

Ou seja, se a distância do planeta ao Sol no afélio for 5% maior que no periélio, podemos ver que a sua velocidade, quando estiver no periélio, será 5% maior:

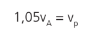
Kepler publicou essas duas leis em seu livro “Astronomia Nova” em 1609. Quase uma década depois, perto da sua morte, publicou a 3^a Lei. Ele sempre tentou buscar uma regularidade com os raios médios das órbitas e o período de revolução dos planetas, até que, em 1618, conseguiu o que tanto buscava:

3^a LEI DE KEPLER OU LEI DOS PERÍODOS

“Os quadrados dos períodos de revolução de dois planetas quaisquer estão entre si como os cubos de suas distâncias médias ao Sol.”
Ou seja:

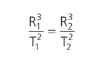
Na mesma época, outro grande nome que se dedicou à ciência foi Galileu. Aperfeiçoou o telescópio, realizando uma série de descobertas. Verificou que a Lua não era uma esfera perfeita. Apresentava uma série de irregularidades em sua superfície. Descobriu os 4 satélites de Júpiter e mediu os seus períodos de revolução. Descobriu as fases de Vênus (movimento similar ao da Lua, devido ao seu posicionamento relativo ao Sol).

Em 1633, foi condenado pela Igreja a ficar em sua casa perpetuamente após se redimir pelos seus “erros e heresias”. Em 1642, após todas essas descobertas, nasceu Isaac Newton. Não seria possível, neste módulo, falar toda a contribuição de Newton para a ciência; precisar-se-ia de um livro inteiro. Vamos nos ater apenas a algumas das contribuições de Newton na gravitação.

Aplicando a 2^a Lei de Newton em um planeta de massa m que realiza uma trajetória (aproximadamente) circular ao redor do Sol (massa M), temos que:

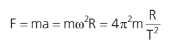
Esse o módulo da força que o Sol exerce no planeta aponta para o centro da trajetória (resultante centrípeta).
Como:

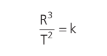
A relação acima proposta por Kepler é constante para todos os planetas. Logo:

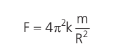
Mostrando, assim, que a força é inversamente proporcional ao quadrado da distância. Além disso, pela 3^a Lei de Newton, a força que o Sol faz em um planeta é igual ao que o planeta faz no Sol, em módulo, concluindo que a sua magnitude depende não só da massa do planeta, mas do produto entre a massa do planeta e a do Sol, chegando à expressão abaixo:

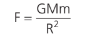
Em que G é a constante universal. Esta é a Lei de Newton da gravitação. Os estudos de Newton sobre corpos celestes (mecânica celeste) são fascinantes, mas vamos nos restringir, para sermos objetivos, à lei acima. Podemos inferir, através de sua lei, que a aceleração resultante, que os planetas sofrem devido exclusivamente ao Sol, centrípeta, nada mais é que a gravidade gerada pelo Sol no ponto onde o planeta se encontra. Logo:

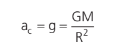
Generalizando essa relação, qual seria a gravidade em um ponto a uma distância R (sendo R o raio da Terra) da superfície da Terra (desconsidere a atuação de campos gravitacionais de outros planetas e do Sol nesse ponto)?

Resolução:

Como quem gera o campo gravitacional é a Terra, basta substituirmos a massa do Sol pela da Terra na expressão acima:

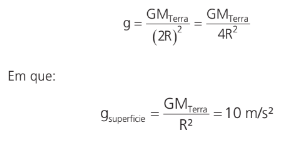
Perceba que a distância entre o C.M. da Terra e do ponto é 2R. Considerando que o raio médio da Terra é de, aproximadamente, 6370 km, um corpo a 6370 km da superfície da Terra sofre uma gravidade 1⁄4 da superfície da Terra, ou seja, aproximadamente 2,5 m/s².

VELOCIDADE DE ESCAPE

Vamos imaginar um foguete saindo da ação gravitacional terrestre (assunto discutido na leitura opcional do módulo anterior). Como o campo gravitacional é conservativo, podemos falar que a energia mecânica do foguete na superfície terrestre é igual a sua energia mecânica quando está a uma distância R → ∞, onde não teria mais a ação gravitacional (“escapou” da Terra).

O problema é que não podemos falar que a energia potencial gravitacional vale mgh, já que a gravidade depende da distância do foguete até o centro da Terra. Quando falamos de um corpo caindo do alto de um prédio, essa preocupação não existe, uma vez que a gravidade é a mesma, tanto no alto do prédio quanto no solo (pensando no ponto mais alto da Terra, o monte Everest, com uma altura de mais de 8 Km, como o raio da Terra é de aproximadamente 6370 km, podemos afirmar que a gravidade é praticamente igual a do nível do mar).

Lembrando que, em um sistema conservativo, temos que:

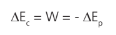
E que o trabalho da força (que, nesse caso é gravitacional) é dado pela equação abaixo:

Como essa força aponta para o centro da trajetória e o vetor raio aponta para fora (no caso, da Terra até a posição do foguete), o ângulo entre os vetores vale 180°. Ou seja, após realizar esse produto escalar, aparecerá um sinal negativo, já que cosseno de 180° vale – 1 (produto escalar e vetorial estão discutidos no módulo de vetores. Caso necessário, consulte-o).

Considerando r₀ = R (distância inicial entre o foguete e o centro da Terra) e R → ∞, teremos:

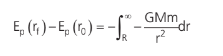
Nesse caso, costuma-se tomar a energia potencial no infinito como zero (lembre-se que podemos tomar qualquer ponto como potencial zero. O que interessa é a diferença de energia potencial. Nos casos de queda livre, costumamos considerar potencial zero no ponto mais baixo, geralmente no solo, conforme fizemos no módulo de energia).

Sendo assim, a energia potencial na superfície da Terra vale:

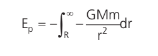
Resolvendo a integral acima chegaremos à expressão abaixo:

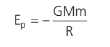
Essa é a energia potencial que um corpo de massa m sofre na superfície de outro de massa M. De modo geral, temos que a energia potencial gravitacional de um corpo a uma distância r qualquer em relação ao outro vale:

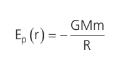
Note que, conforme um corpo cai em queda livre, a sua energia potencial diminui (aproxima-se da Terra). O sinal de menos acima pode ser explicado pelo fato de, conforme o corpo vai se afastando do planeta, a sua energia potencial deve aumentar, o que, de fato, acontece. O gráfico abaixo mostra isso mais claramente:

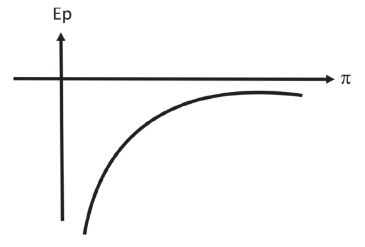
Agora que sabemos a expressão de energia potencial, vamos voltar ao nosso foguete escapando da Terra. Vamos considerar que gastou toda a sua energia para escapar do planeta. Sendo assim, a soma das energias potencial e cinética iniciais do foguete deve ser igual à mecânica final, que é zero. Logo:

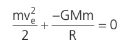
Em que v_e é a velocidade inicial do foguete, chamada de velocidade de escape. Então:

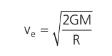
Podemos substituir com a expressão da gravidade:

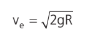
No caso da Terra (R ~6,4.10⁶ m), a velocidade mínima para escapar do planeta será:

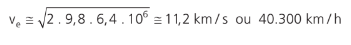
VELOCIDADE ORBITAL

Qual é o módulo da velocidade que um corpo de massa m tem quando está em órbita a uma distância r de um planeta de massa M? Qual é a velocidade orbital da Terra ao redor do Sol? Basta lembrarmos que o módulo da aceleração centrípeta é equivalente à gravidade local, gerada por M:

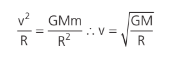
Essa é a velocidade orbital do corpo de massa m. A distância média entre a Terra e o Sol é de aproximadamente 1,5.10¹¹ m e M = 2.10³⁰ Kg (massa do Sol). Com esses dados, podemos calcular a velocidade orbital da Terra:

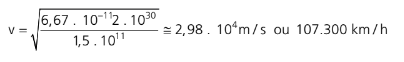
Essa é a velocidade média com que a Terra realiza o seu movimento de translação. Lembrando que é média, já que, quando a Terra está no seu periélio, a velocidade é ligeiramente maior e, quando está no
afélio, um pouco menor.

Problema do lixo espacial: milhares de detritos estão, nesse momento, orbitando ao redor da Terra. Objetos de tamanhos variados. A maioria tem poucos centímetros, mas estão em altas velocidades, podendo causar complicações no momento de decolagem ou aterrissagem de uma nave, por exemplo, ou até mesmo destruir uma base ou satélite.

Vamos imaginar um objeto de 10 cm que está a 600 Km da superfície terrestre, ou seja, a aproximadamente 7000 Km do centro da Terra. Sabendo-se que a massa da Terra é de, aproximadamente, 6.1024 Kg, teremos que:

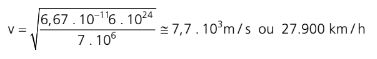
São objetos a incrível velocidade de quase 30.000 km/h! Repare o tempo que esse objeto leva para dar uma volta na Terra:

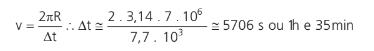
Após o lixo passar em certo ponto (na verdade, é uma camada de quilômetros de lixo), podemos dizer, de modo aproximado, que há uma janela de 1h30min para atravessar a região.

GRAVIDADE NO INTERIOR DE UM PLANETA

Sabemos a expressão da gravidade a uma distância r do centro de um planeta. E, se estivéssemos a uma distância r < R (R = raio do planeta)? Podemos fazer uma analogia com a questão do campo elétrico a uma distância r < R em uma esfera isolante de carga Q. Podemos criar uma espécie de gaussiana, na qual apenas a massa dentro dessa superfície faria campo gravitacional no ponto:

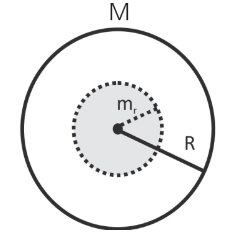
Vamos chamar de m a massa dentro da região pontilhada da figura. Então:

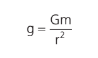
Considerando a densidade do planeta uniforme, temos que:

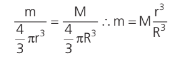
Logo:

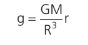
Perceba o caráter linear da função. A gravidade aumenta linearmente com a distância, até que r = R. A partir desse ponto, a gravidade diminui com o inverso do quadrado da distância, caracterizando uma hipérbole, conforme mostra o gráfico g x r abaixo:

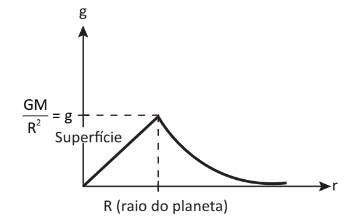
Observação

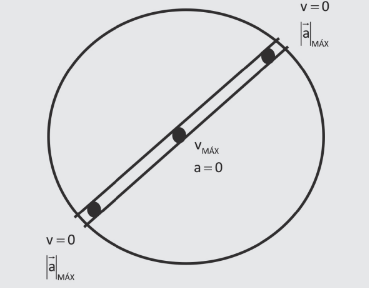
No interior de um planeta, como a aceleração local é proporcional à distância, se fosse possível cavar um túnel de uma ponta a outra do diâmetro do planeta e colocássemos um corpo de massa m para se locomover ao longo do túnel, o seu movimento seria um M.H.S., cuja velocidade seria zero quando chegasse à superfície e seria máxima no centro do planeta, assim como a aceleração seria máxima na superfície, como vimos, e zero no seu centro.

APÊNDICE

Porém, como aplicar a 3^a Lei se as trajetórias forem elípticas?

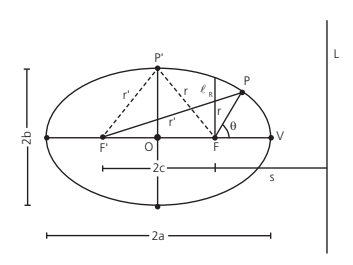
Na figura acima, temos que a é o semieixo maior da elipse. Com um pouco de conta (conhecimento de área de elipse, momento angular e massa reduzida), podemos chegar à relação abaixo (que é a 3^a lei de Kepler):

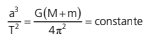
Conclusão, quanto maior o semieixo maior, maior será o período orbital.

Exercício Resolvido

Resolução: D

Como o semieixo maior do satélite 1 tem o mesmo comprimento que o raio da trajetória circular do satélite 3, terão o mesmo período orbital. Já o satélite 2, seu semieixo maior a₂ é maior que o semieixo maior que o do satélite 1, logo, terá um período maior que os demais.