CONE
CONCEITO
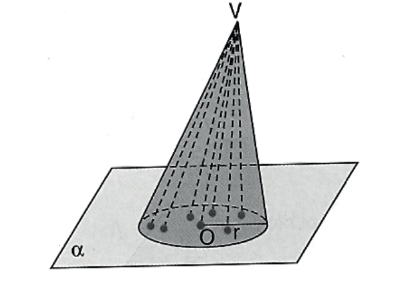
Consideremos um círculo de centro O e raio r, situado num plano α, e um ponto V fora de α. Chama-se cone circular, ou cone, a reunião dos segmentos com uma extremidade em V e a outra em um ponto do círculo.
ELEMENTOS
Considerando o cone representado a seguir, temos:
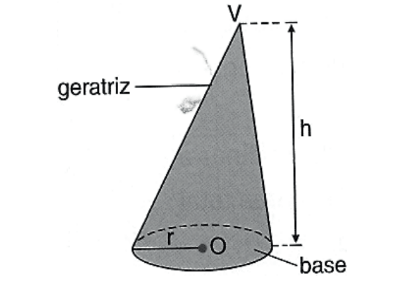
• O ponto V é o vértice do cone
• O círculo de raio r é a base do cone
• Os segmentos com uma extremidade em V e a outra nos
pontos da circunferência da base são as geratrizes do cone
• A distância do vértice ao plano da base é a altura do cone
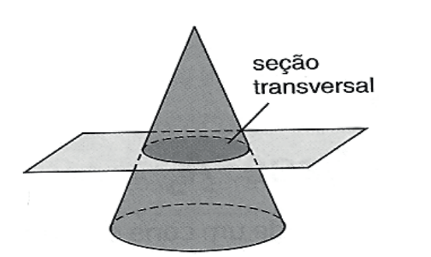
• Secção transversal de um cone é qualquer interseção não vazia do cone com um plano paralelo à base (desde que este não passe pelo vértice); trata-se de um círculo.
CLASSIFICAÇÃO
Um cone pode ser classificado conforme a inclinação da reta VO sendo ‘O’ o centro da base, em relação ao plano da base:
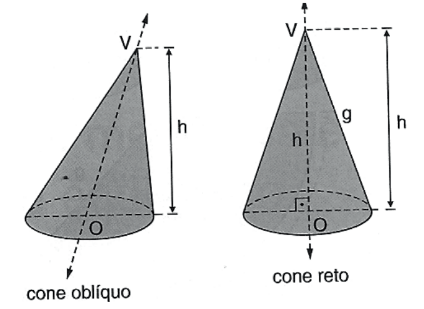
• O cone circular é obliquo quando a reta VO é oblíqua à base;
• O cone circular é reto quando a reta VO é perpendicular à base
ÁREAS

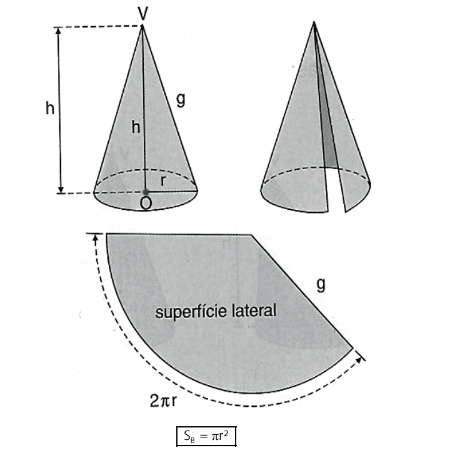

A planificação da superfície lateral (ou a reunião das geratrizes) de um cone nos dá um setor circular com as seguintes características:
• Raio: g (geratriz do cone)
• Comprimento do arco: 2πr (perímetro da base)
A área lateral do cone é dada por:
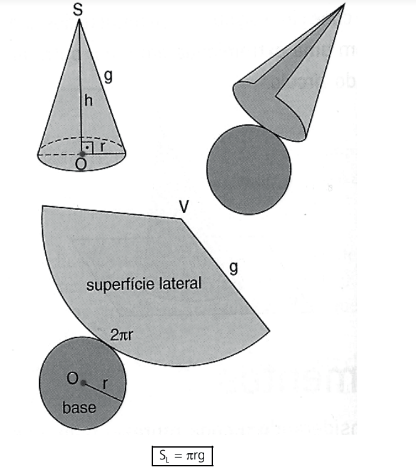

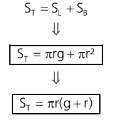
Superfície total de um cone é a reunião da superfície lateral com o círculo da base. A área dessa superfície é chamada área total.
VOLUME
O volume de um cone vale um terço do produto da área da base pela altura:
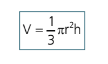
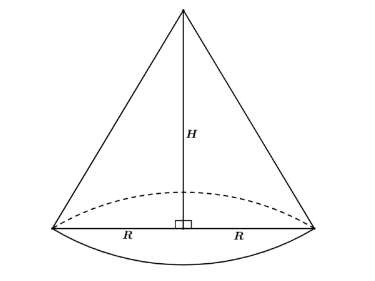
SEÇÃO MERIDIANA E CONE EQUILÁTERO
Seção meridiana de um cone é a intersecção dele com um plano que contém o eixo. A seção meridiana de um cone reto é um triângulo equilátero.

Cone equilátero é um cone cuja seção meridiana é um triângulo equilátero. Assim

ESFERA
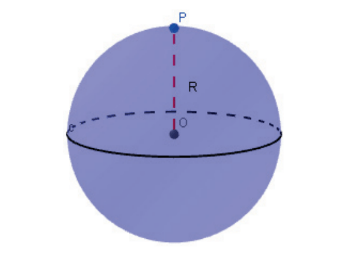
Chama-se esfera a um sólido limitado por uma superfície em que todos os pontos de um ponto interior chamado de centro.
A superfície que delimita a esfera, denomina-se: superfície esférica e qualquer segmento OP que une o centro O com um ponto P da superfície esférica denomina-se raio da esfera.
ÁREA DA SUPERFÍCIE ESFÉRICA DE RAIO R

VOLUME DA ESFERA

FUSO E CUNHA ESFÉRICA
Denomina-se fuso esférico a superfície gerada pela rotação de uma circunferência que gira um ângulo α menor que 2π radianos ao redor do seu diâmetro.
Chama-se cunha esférica ao sólido gerado pela rotação, de um ângulo α, menor que 2π radianos, de um semicírculo, ao redor do seu diâmetro.
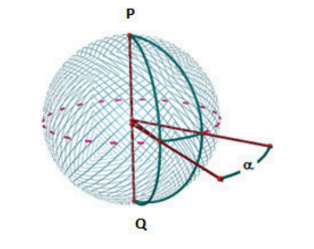
A área do fuso esférico e o volume da cunha esférica são proporcionais ao ângulo do fuso (α).
Área do fuso esférico de ângulo α radianos:
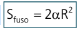
Volume da cunha esférica de ângulo α radianos:
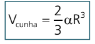
SEGMENTO E CALOTA ESFÉRICA
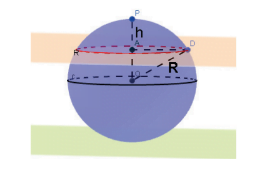
Quando seccionamos uma esfera por um plano e um outro plano tangencia a esfera, o plano secante divide a esfera em dois segmentos esféricos, e a superfície esférica em duas calotas esféricas.
VOLUME DO SEGMENTO ESFÉRICO
De modo análogo ao volume da esfera, podemos calcular o volume do segmento esférico de altura h subtraindo um tronco de cone de altura h, de um cilindro de raio R e também altura h.
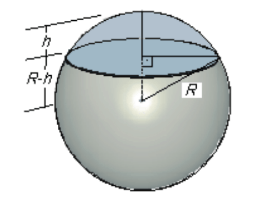
Volume do segmento esférico de altura h em uma esfera de raio R:
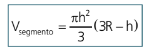
Área da calota esférica de altura h em uma esfera de raio R:
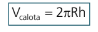
TRONCOS DE SÓLIDOS
SÓLIDOS HOMOGÊNEOS
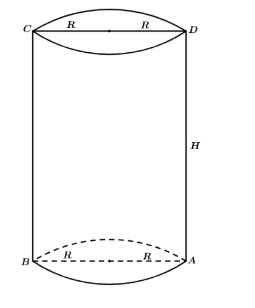
Nosso estudo irá focar nos cortes de sólidos, cortes esses feitos por planos paralelos as bases.
Primeiramente vamos pensar o seguinte: por que vemos tantas questões que envolvem apenas troncos de pirâmides ou cones? A resposta acaba sendo simples, esses tipos de sólidos são aqueles que quando seccionados por um plano paralelo a base geram maiores investigações. Sabemos, do dia a dia inclusive, que quando temos sólidos homogêneos, cubos, paralelepípedos, prismas retos ou cilindros retos, que quando queremos tomar uma porção de seu volume basta tomarmos a mesma fração da altura que queremos de volume. Veja abaixo.
Temos um cilindro circular reto e vamos fazer um corte utilizando um plano paralelo as bases exatamente na metade da sua altura.
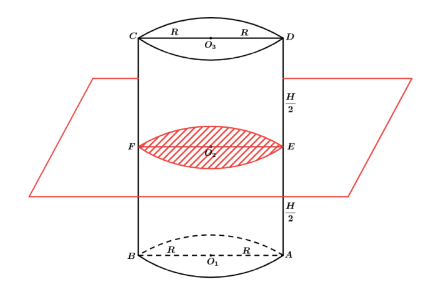

porém, pelo fato de ser um sólido homogêneo, qualquer corte por um plano paralelo as bases irá gerar o mesmo polígono das bases e de mesma área S.
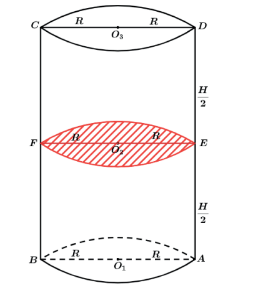

Não é à toa que se uma receita pede que seja utilizado metade do volume de uma lata de leite condensado nós utilizamos o leite condensado até a metade da lata. Se enchermos um cubo até um terço de sua altura teremos um terço do volume total e assim para qualquer sólido homogêneo.
ProBizu
Nos sólidos homogêneos os cortes em diagonal também geram metade do volume.
Cada sólido resultante tem metade do volume do sólido original.
PIRÂMIDES E CONES
O estudo para as pirâmides retas e cones retos se dá da mesma maneira quando seccionados por planos paralelos a suas bases.
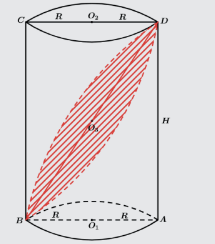
Utilizando a mesma ideia dos sólidos homogêneos fica fácil perceber que após um corte por um plano paralelo a base os sólidos resultantes não terão seus volumes ligados diretamente a proporção de suas alturas. Dessa forma temos de recorrer a semelhança entre os sólidos. Tomemos o cone reto abaixo.
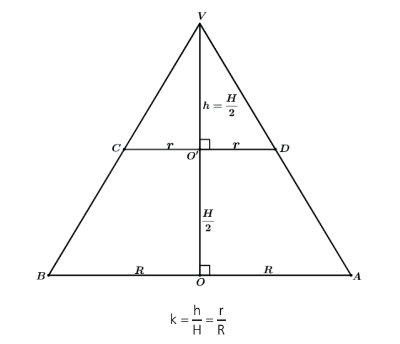
Vamos fazer uma secção por um plano paralelo a base de centro O do cone.
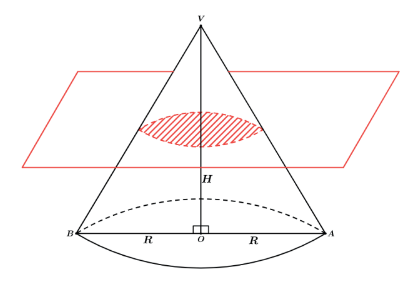
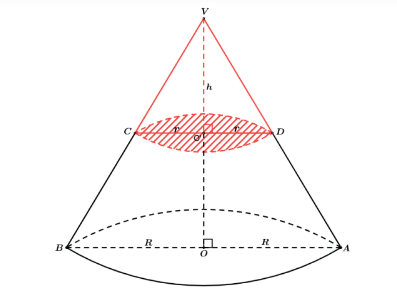
Vemos que o novo cone gerado, VCD de centro O’, também tem como base um círculo, porém de raio diferente do cone VAB de centro O. Dessa forma seu volume não fica dependendo somente de sua altura h como também passa a depender desse seu novo raio da base r, que é definido através de uma semelhança.
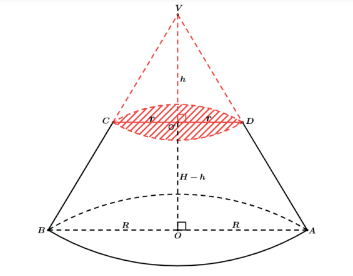
Tronco é o sólido resultante da retirada do sólido superior ao plano de corte (sólido que é semelhante ao sólido original). Vale lembrar que os troncos eles não são sólidos semelhantes com os sólidos originais ou os retirados, utilizá-los na semelhança é um erro muito comum.
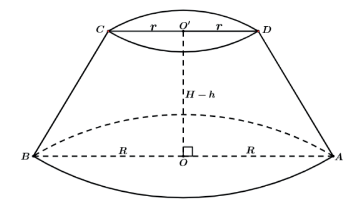
A figura acima ilustra um tronco de cone reto, resultado da remoção do cone menor do cone maior.
Chegaremos ao seu volume utilizando semelhança entre os sólidos encontrando os volumes do sólido maior e do menor e no final fazendo a diferença entre seus volumes.
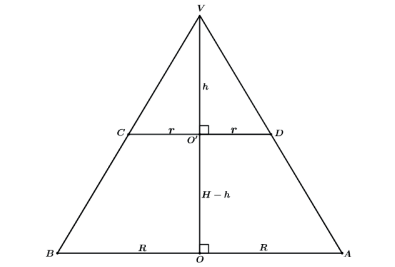
Vamos “ver” de frente os sólidos e ver os triângulos que temos. Quando fazemos a semelhança de medidas lineares, medidas de comprimento, apenas uma dimensão, dizemos que essa razão de semelhança é k. Assim para os triângulos da figura teríamos
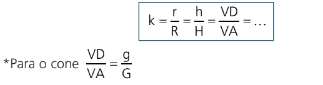

Dessa forma podemos fazer razões entre os volumes dos sólidos VCD e VAB.
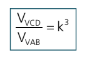
Assim para encontrarmos k basta utilizarmos a razão que nos for
Depois de encontrado o volume do sólido “menor” para encontrarmos o volume do tronco basta efetuar a subtração entre os volumes dos cones “maior” e “menor”.
Exemplo:
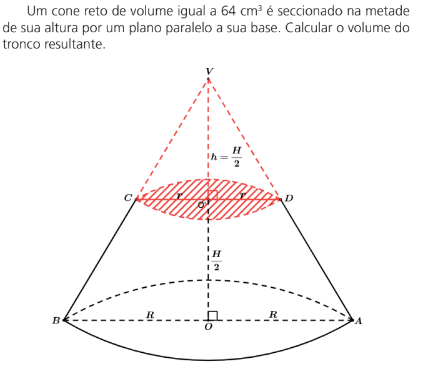
Ao utilizarmos a subtração teremos

Assim fazendo a semelhança entre os volumes dos 2 cones

Existem 2 fórmulas que calculam direto os volumes do tronco de cone e de pirâmide quando são conhecidas as medidas das 2 bases e da altura do tronco.
I. Tronco de cone
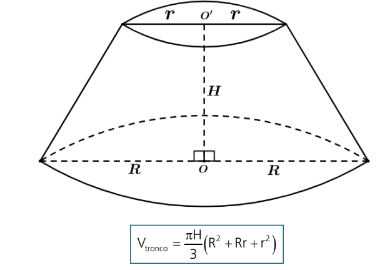
R → Raio da base maior
r → Raio da base menor
H → Altura do tronco
II. Tronco de pirâmide
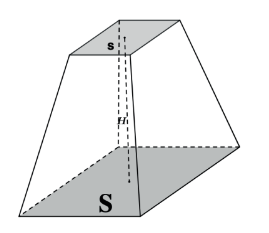
- A fórmula serve para troncos de pirâmides retas de qualquer base, a figura utilizou a quadrangular só para exemplificar.
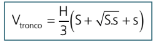
S → Área da base maior
s → Área da base menor
H → Altura do tronco
INSCRIÇÃO E CIRCUNSCRIÇÃO DE SÓLIDOS
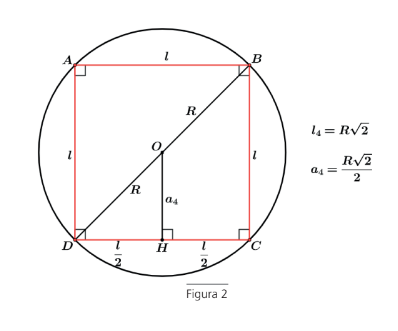
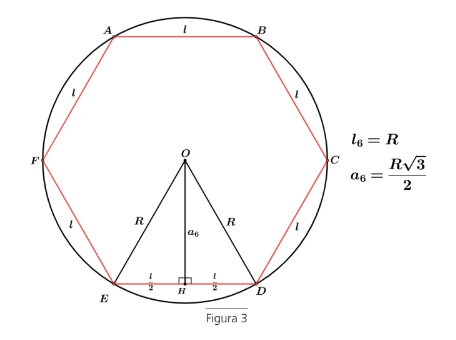
REVISÃO – PRINCIPAIS POLÍGONOS REGULARES INSCRITOS
PIRÂMIDE REGULAR INSCRITA EM UM PRISMA REGULAR DE MESMA BASE


PIRÂMIDE REGULAR INSCRITA EM UM PRISMA REGULAR DE BASE DIFERENTE

Ou seja, a razão entre os volumes será o triplo da razão entre as áreas das bases.
Vamos mostrar alguns casos
I. Pirâmide triangular regular inscrita num prisma hexagonal regular
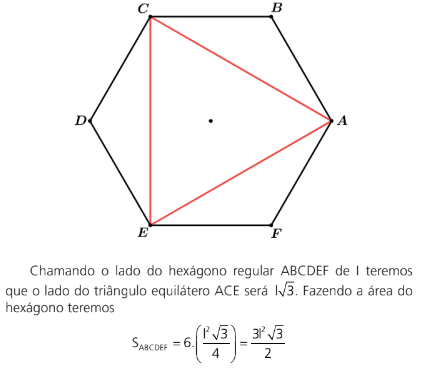
Teremos a área do triângulo equilátero
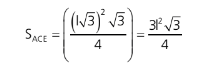
Assim vemos que a área do hexágono regular é o dobro da área do triângulo equilátero. Sendo o hexágono regular a base do prisma regular e o triângulo equilátero a base da pirâmide regular teremos que

II. Pirâmide quadrangular regular inscrita num prisma triangular regular
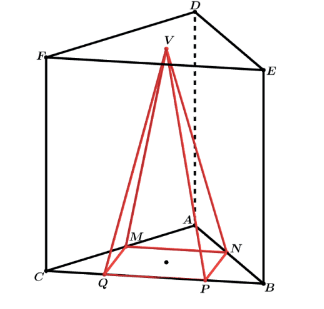

Sendo o lado do triângulo equilátero ABC igual a l e o lado do quadrado MNPQ igual a x montaremos as razões entre os triângulos semelhantes AMN e ABC.
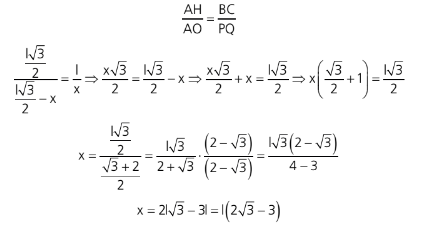
Assim a área do quadrado MNPQ será

Assim a razão entre os volumes do prisma e da pirâmide será
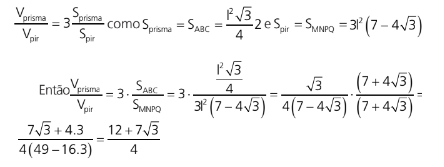
PRISMA REGULAR INSCRITO EM UM CILINDRO RETO
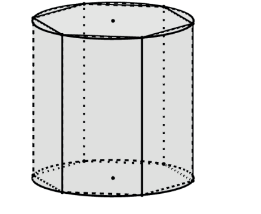
A razão entre os volumes do cilindro reto e do prisma regular inscrito em sua base dar-se-á por
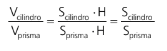
Teremos então que a razão entre os volumes será dada pela razão entre as áreas das bases, que com a ajuda da revisão dos principais polígonos regulares inscritos poderemos definir para os principais prismas regulares retos.
I. Prisma triangular regular inscrito no cilindro reto

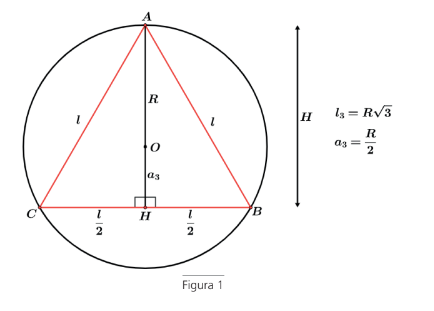
A relação entre o lado do triângulo inscrito e o raio do círculo circunscrito é dado por ( figura 1)
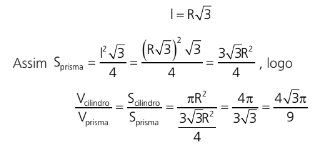
III. Prisma triangular regular inscrito no cilindro reto

A relação entre o lado do hexágono inscrito e o raio do círculo circunscrito é dado por ( figura 3)
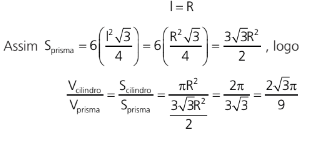
PIRÂMIDE REGULAR INSCRITA EM UM CILINDRO RETO
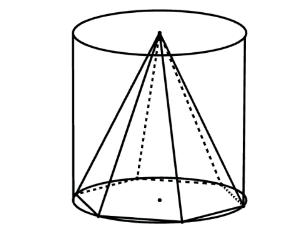
De maneira análoga ao item anterior teremos
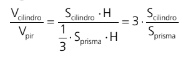
Então vemos que temos o triplo das razões anteriores, assim
I. Pirâmide triangular regular inscrita no cilindro reto
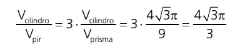
II. Pirâmide quadrangular regular inscrita no cilindro reto
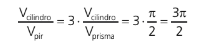
III. Pirâmide triangular regular inscrita no cilindro reto
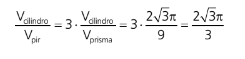
PIRÂMIDE REGULAR INSCRITA EM UM CONE RETO
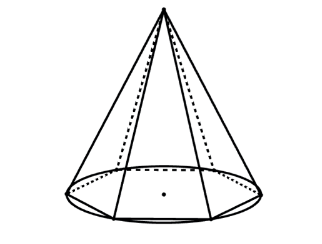

I. Pirâmide triangular regular inscrita no cone reto
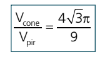
II. Pirâmide quadrangular regular inscrita no cone reto
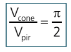
III. Prisma triangular regular inscrita no cone reto
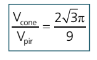
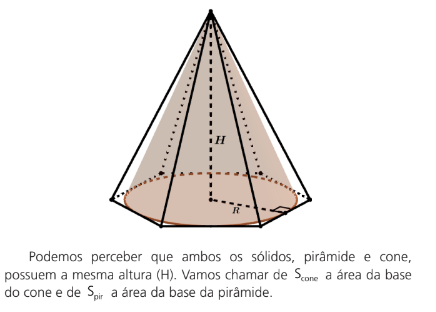
CONE RETO INSCRITO EM UMA PIRÂMIDE REGULAR
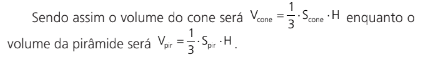
Fazendo a razão entre os volumes da pirâmide e do cone teremos:
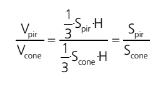

O que nos faz concluir que a razão entre os volumes é a razão entre os perímetros das bases.
OCTAEDRO FORMADO PELOS CENTROS DAS FACES DE UM CUBO
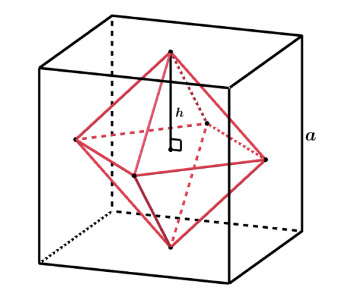
Vamos ligar 2 centros de faces laterais consecutivas do cubo.
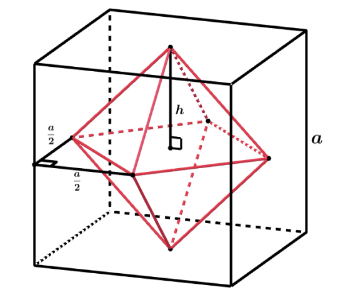
Agora temos o triângulo retângulo indicado na figura e dessa forma podemos calcular a aresta do octaedro regular em função da aresta a do cubo. Vamos chamar a aresta do octaedro regular de x.
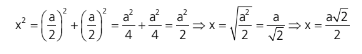
Dessa forma o volume do octaedro regular será o dobro do volume de uma das pirâmides quadrangulares regulares que o formam.
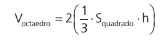

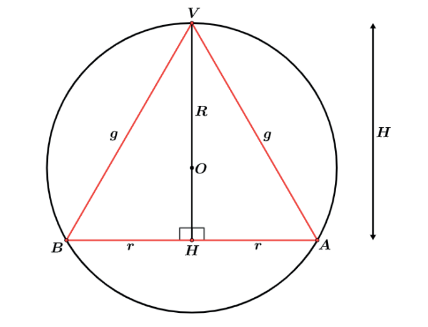
CONE RETO INSCRITO NA ESFERA
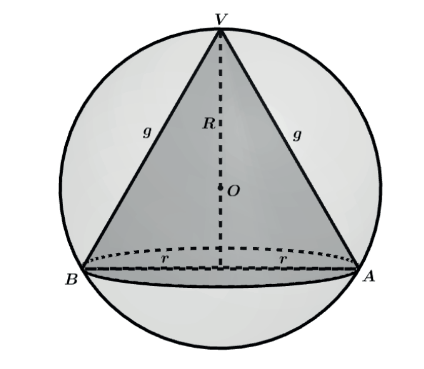
Podemos fazer a assimilação do triângulo inscrito no círculo.

ProBizu
No caso do cone equilátero podemos imaginar o caso do triângulo equilátero inscrito no círculo de raio R, onde
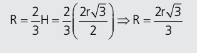
CILINDRO RETO INSCRITO NA ESFERA
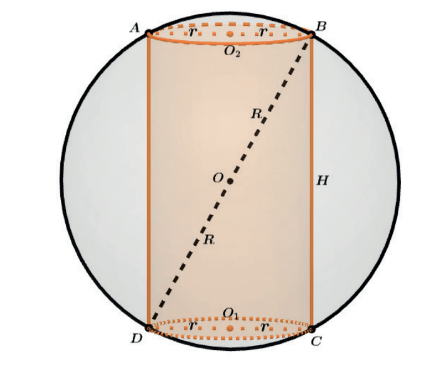
Neste caso podemos fazer a vista frontal e utilizarmos a ideia de um retângulo inscrito num círculo de raio R.
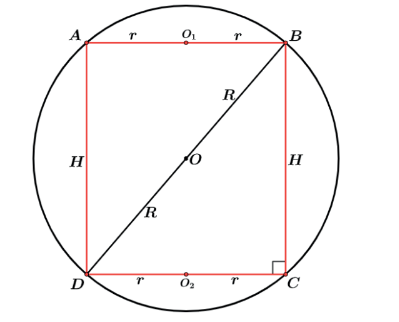
Assim podemos relacionar nossos elementos aplicando o Teorema de Pitágoras no triângulo retângulo BCD.
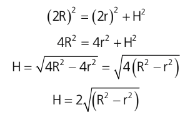
ProBizu
No caso do cilindro equilátero podemos imaginar o caso do quadrado inscrito no círculo de raio R, onde teremos:
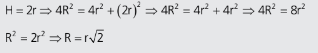
ESFERA INSCRITA NO CONE RETO
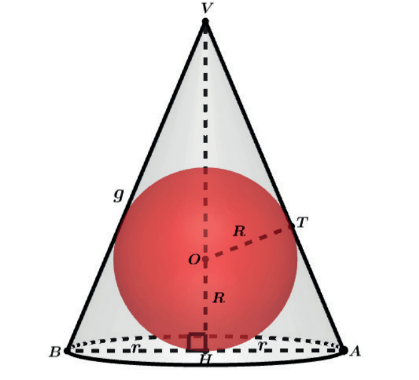
Podemos fazer a assimilação do triângulo circunscrito ao círculo.
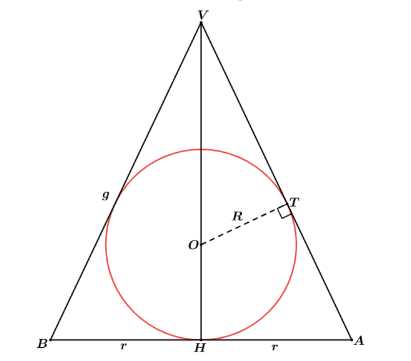

ProBizu
No caso do cone equilátero podemos imaginar o caso do triângulo equilátero circunscrito ao círculo de raio R, onde g 2r = e
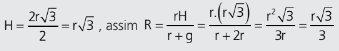
ProBizu
A esfera só pode ser inscrita no cilindro equilátero.
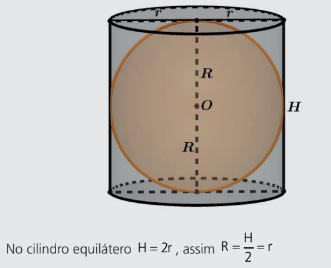
CUBO INSCRITO NA ESFERA
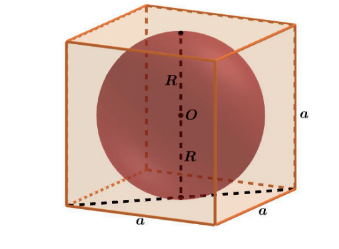
ESFERA INSCRITA NO CUBO

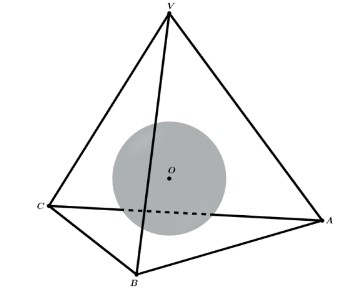
ESFERA INSCRITA NO TETRAEDRO REGULAR
Seja uma esfera de centro O inscrita em um tetraedro regular VABC como na figura.
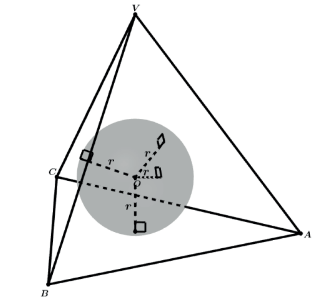
Ao traçarmos as distâncias do centro O da esfera as 4 faces VAB, VAC, VBC e ABC do tetraedro regular teremos todas essas 4 distâncias iguais ao raio da esfera (r).

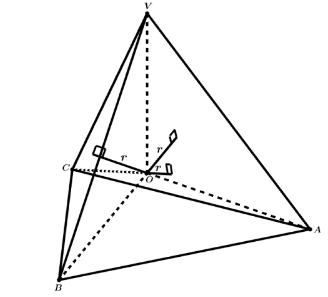
As bases VAB, VBC, VCA e ABC são todas de mesma área, pois são os mesmos triângulos equiláteros que formam o tetraedro regular VABC.
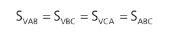
Assim podemos concluir que o volume do tetraedro VABC pode ser decomposto no volume dos tetraedros OVAB, OVBC, OVCA e OABC.

Exercício Resolvido
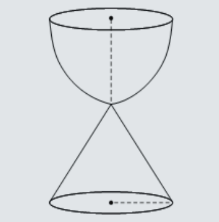
- Um artesão resolveu fabricar uma ampulheta de volume total V constituída de uma semiesfera de raio 4 cm e de um cone reto, com raio e altura 4 cm, comunicando-se pelo vértice do cone, de acordo com a figura abaixo.

Resolução: A
O resultado pedido é dado por
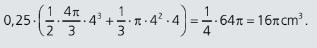
Exercício Resolvido
- Um torneiro mecânico construiu uma peça retirando, de um cilindro metálico maciço, uma forma cônica, de acordo com a figura 01 a seguir:
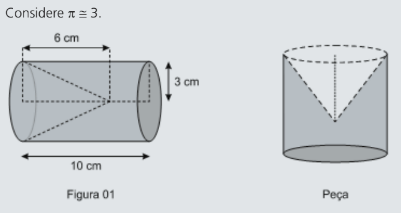
Qual é o volume aproximado da peça em milímetros cúbicos?
Resolução: A
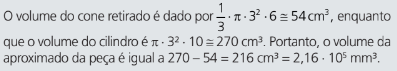
Exercício Resolvido
- Um cone circular reto, cuja medida do raio da base é R, é cortado por um plano paralelo a sua base, resultando dois sólidos de volumes iguais. Um destes sólidos é um cone circular reto, cuja medida do raio da base é r. A relação existente entre R e r é:
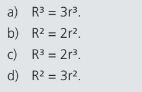
Resolução: C
Sejam v e 2v, respectivamente, o volume do cone de raio r e o volume do cone de raio R.

- Uma indústria de bebidas criou um brinde para seus clientes com a forma exata da garrafa de um de seus produtos, mas com medidas reduzidas a 20% das originais. Se em cada garrafinha brinde cabem 7 ml de bebida, podemos concluir que a capacidade da garrafa original é de:
a) 875 ml
b) 938 ml
c) 742 ml
d) 693 ml
e) 567 ml
Resolução: A
Seja C a capacidade da garrafa original, em mililitros. Como os sólidos são semelhantes, tem-se que
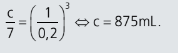
Exercício Resolvido
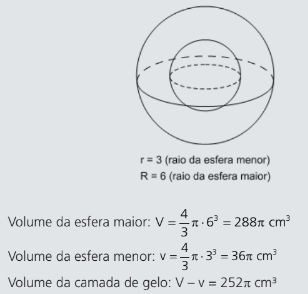
- Uma esfera metálica de 3 cm de raio é colocada em um congelador e, após algum tempo, acumula uma camada de gelo de 3 cm de espessura, mantendo a forma esférica. Então, o volume do gelo acumulado é

Resolução: C