O PLANO CARTESIANO
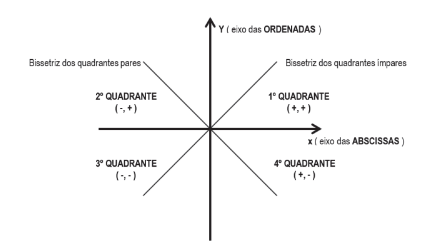
A cada ponto P do plano cartesiano corresponde um par ordenado (x, y) de números reais e escrevemos P(x, y) para indicar este ponto.
Dois eixos orientados (x e y) são dispostos ortogonalmente, dando a origem à divisão do plano em quatro partes, cada uma denominada quadrante. Os quatro quadrantes são numerados no sentido anti- horário, e os eixos e a intersecção entre eles são denominados, respectivamente, eixo das abscissas (x), eixo das ordenadas (y) e origem (0) do sistema de coordenadas cartesianas.
A reta que divide ao meio os quadrantes ímpares é chamada de bissetriz dos quadrantes ímpares e a que divide os quadrantes pares é a bissetriz dos quadrantes pares.
Qualquer ponto P no plano cartesiano terá coordenadas.

A equação de reta da bissetriz dos quadrantes ímpares é x = y enquanto a equação da bissetriz dos quadrantes pares é x = –y.
Observações:


PONTO MÉDIO E DISTÂNCIA
Vamos começar nossos estudos em apenas uma dimensão.

Vamos primeiramente definir distância em apenas uma dimensão.


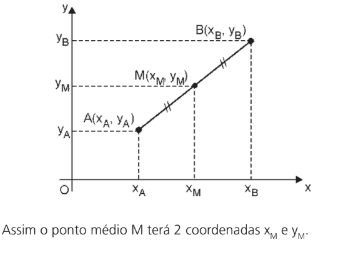
Assim para 2 dimensões, para o plano xy, basta fazermos o ponto médio em relação ao eixo x e o ponto médio em relação ao eixo y.
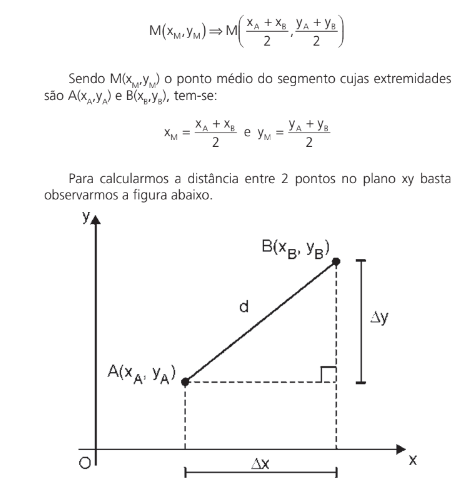

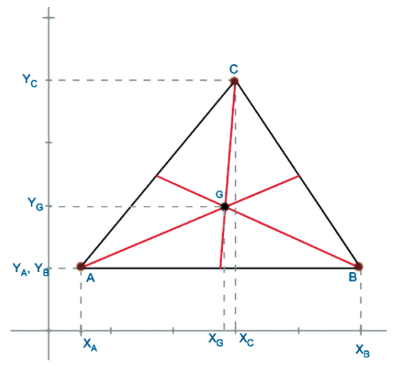
BARICENTRO DE UM TRIÂNGULO
Baricentro é o ponto de encontro de todas as medianas de um triângulo. Lembre-se que o baricentro sempre divide a mediana na razão de 2:1. A distância do vértice ao baricentro (G) é o dobro da distância do baricentro ao lado.

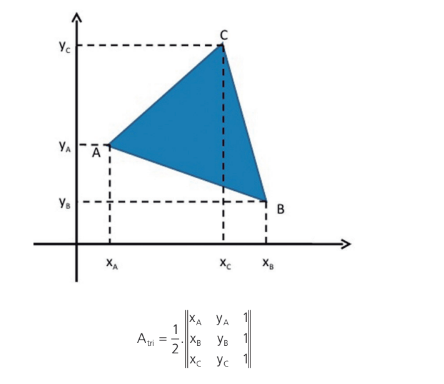
ÁREA DO TRIÂNGULO
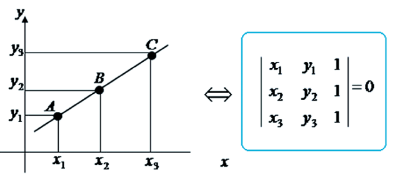
CONDIÇÃO DE ALINHAMENTO DE TRÊS PONTOS
Podemos pensar que se temos 3 pontos alinhados esses pontos não podem formar um triângulo, logo se não podem formar um triângulo não há área (s = 0). Dessa forma devemos igualar o determinante a 0.
ÁREA DE UM POLÍGONO QUALQUER
Podemos encontrar a área do triângulo a partir das coordenadas dos seus 3 vértices através do seguinte algoritmo.
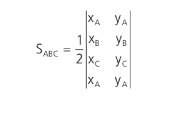
Perceba que a última linha será a coordenada do mesmo ponto utilizado na primeira linha. Assim para calcularmos a área de um triângulo teremos 4 linhas, um quadrilátero 5 linhas, …, e assim para qualquer quantidade de vértices do polígono.
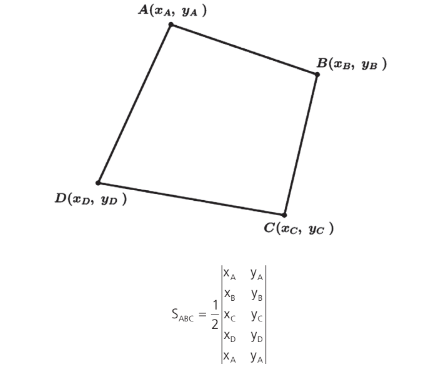
O processo se dá de forma semelhante ao cálculo do determinante

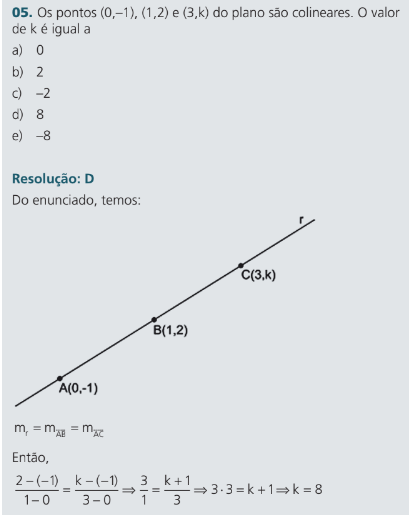
Exercício Resolvido

Exercício Resolvido

Exercício Resolvido

Exercício Resolvido

Exercício Resolvido