DEFINIÇÃO
Sendo x ∈ R, de ne-se módulo ou valor absoluto de x que se indica através da relação.
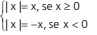
1) o módulo de um número real não negativo é igual ao próprio número.
2) o módulo de um número real negativo é igual ao oposto desse número.
Exemplo:
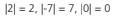
EQUAÇÕES MODULARES
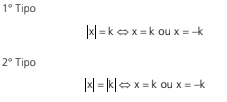
Exemplo 1:
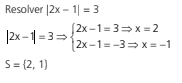
Exemplo 2:
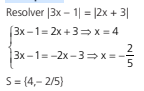
INEQUAÇÕES MODULARES
Podemos interpretar o módulo de um número como sua distância a origem na retal real. Dessa forma sempre que tivermos um número real k haverá o seu simétrico –k que terá a mesma distância a origem
da reta real e dessa forma consequentemente o mesmo módulo.
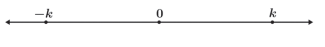
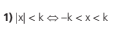
Devemos pensar em todos os números reais que possuem o módulo menor que um número k, que é o mesmo que pensar em todos os números que possuem a distância até a origem da reta real menor que a distância do número k. Assim vemos que se trata da parte interna entre k e –k.
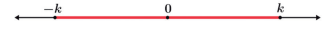
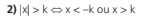
De maneira análoga iremos pensar agora em todos os números reais que possuem a distância até a origem da reta real maior do que o número .
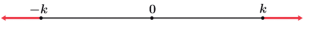
Exemplo 1:
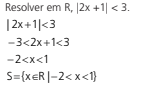
Exemplo 2:
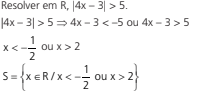
OUTROS TIPOS DE EQUAÇÕES E INEQUAÇÕES MODULARES
Existem outros tipos de equações ou inequações modulares, geralmente quando há alguma operação entre 2 ou mais módulos distintos, onde precisaremos decompor cada módulo individualmente e arrumar em uma tabela para melhor visualização dos intervalos. Mas antes vamos aprender a decompor módulos corretamente.

realmente é estudar o sinal da função que está dentro do módulo para depois decompô-lo.
Veja:
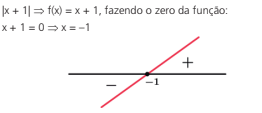
Depois de visto isso vamos ver nossas equações e inequações:
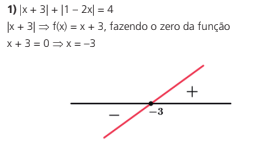
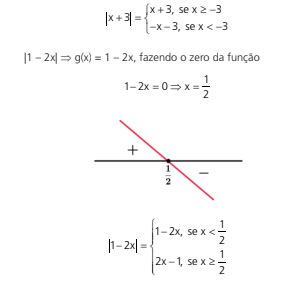
Assim iremos montar uma tabela:





Dessa forma dentre todos os intervalos temos apenas um conjunto unitário como solução, S = {2}.
GRÁFICO DA FUNÇÃO MODULAR
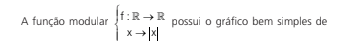

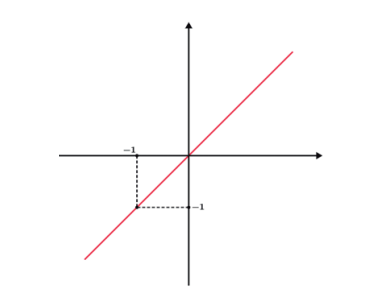
Verificamos que a simetria da parte negativa do gráfico deve ser mantida depois de rebatermos para cima.
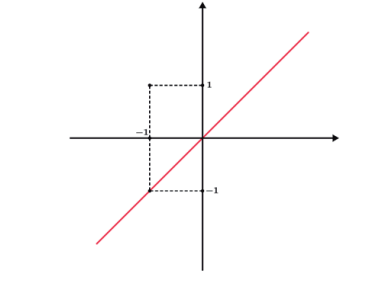
Fazendo f (x) = |g (x)|
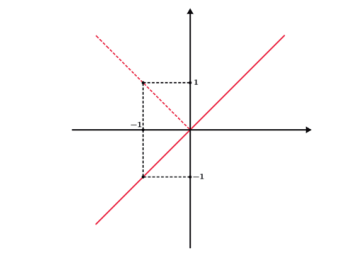
Por fim
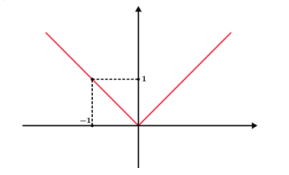
Vamos ver outro exemplo:
2) f (x) = |2x + 1| + 2
Daí podemos dizer que f (x) = |g(x)| + 2 onde g (x) = 2x +1.
Assim traçamos primeiro g (x) = 2x + 1
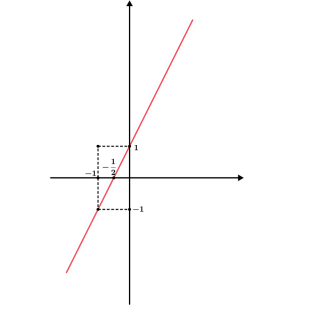
Depois modulamos f (x) = |g (x)|
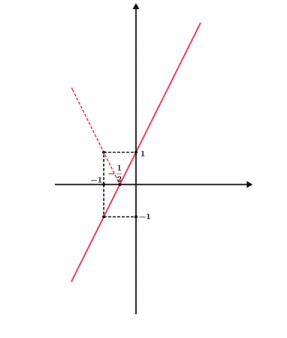
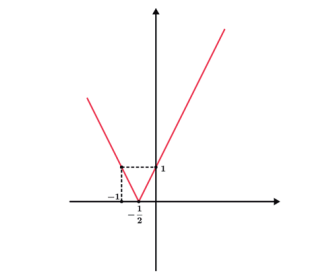
E agora iremos deslocar 2 unidades para cima:
f(x) = |g (x)| + 2
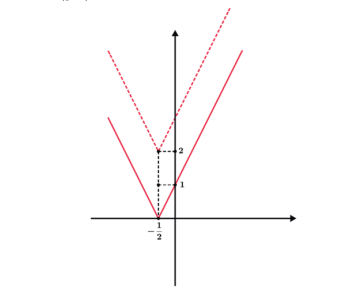
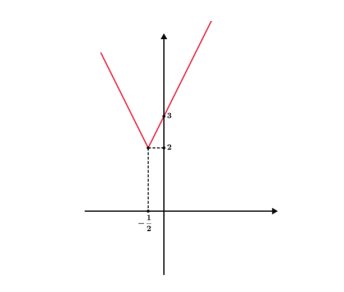
Também podemos traçar o gráfico de funções modulares decompondo os módulos e criando assim funções de sentenças abertas.
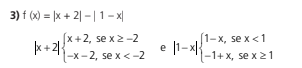
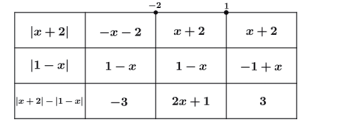
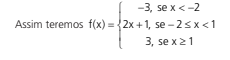
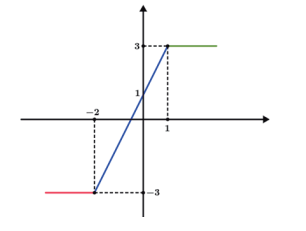

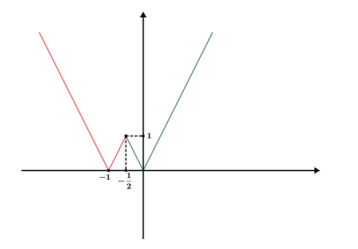
Se quiséssemos poderíamos ter divido mais, veja:
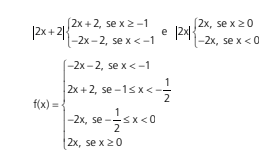
INEQUAÇÕES SIMULTÂNEAS
A dupla desigualdade f (x) < g (x) < h (x), se decompõem em 2 inequações simultâneas
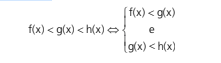
Exemplo:
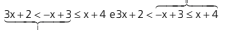
Temos que resolver as 2 inequações
1) 3x + 2 < – x + 3 ⇒ 4x < 1 ⇒ x < 1/4
2) – x + 3 ≤ x + 4 ⇒ –2x ≤ 1 ⇒ x ≥ –1/2
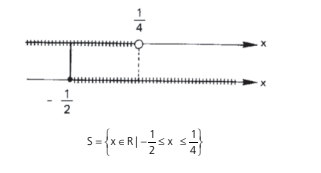
A interseção desses dois conjuntos é
INEQUAÇÕES PRODUTO
Sendo f(x) e g (x) duas funções na variável x, as inequações f(x) g(x) 0, f(x) g(x) 0, f(x) g(x) 0 ×> ×< ×3 e f(x) g(x) 0 × £ são denominadas inequações produto.
Exemplo:
(x + 2) · (2x – 1) > 0. Um processo prático é fazer o estudo de cada
função separadamente. Fazemos o estudo de f(x) = (x + 2) e g(x) = (2x + 1).
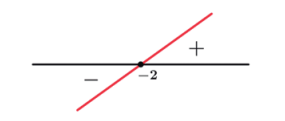
Sinal de f(x) = x + 2
Zero da função: f(x) = 0 ⇒ x + 2 = 0 ⇒ x = –2
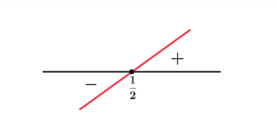
Sinal de g(x) = 2x + 1
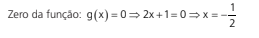
Agora usamos o auxílio do quadro abaixo onde usamos a regra dos sinais para a multiplicação.
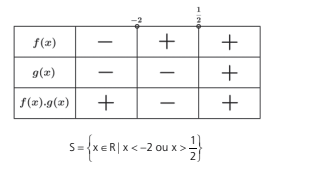
A inequação f(x) · g(x) ≥ 0 tem como solução a união das soluções de f(x) · g(x) > 0 com as soluções de f(x) · g(x) = 0.
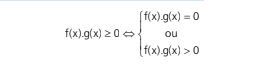
Exemplo:
Resolver a inequação (3x + 1) · (2x – 5) ≥ 0 em R.
Fazemos o estudo de f(x) = (3x + 1) e g(x) = (2x – 5).
Sinal de f(x) = 3x + 1
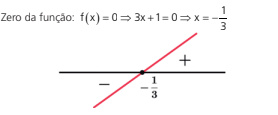
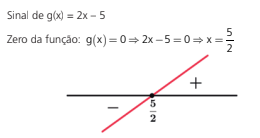
Fazendo o quadro de sinais teremos
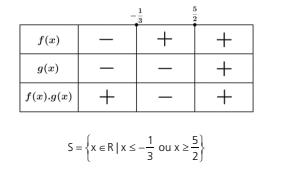

1) toda potência de base real e expoente ímpar conserva o sinal
da base

2) toda potência de base real e expoente positivo resulta num número não negativo.
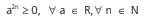
Assim sendo, temos:
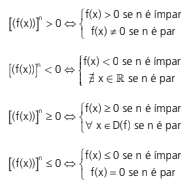
Exemplos:
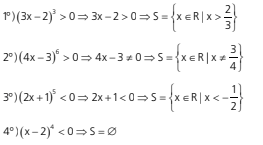
INEQUAÇÕES QUOCIENTE
As regras para se resolver as inequações quociente são as mesmas para as inequações produtos, apenas devemos atentar para as restrições de não se poder deixar zerar o denominador da fração pois não existe divisão por zero.
Exemplo:

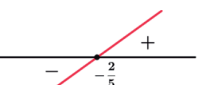
Sinal de g (x) = 1 – x
Zero da função: g(x) = 0 ⇒ 1 – x = 0 ⇒ x = 1
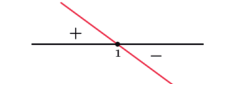
Fazendo o quadro de sinais
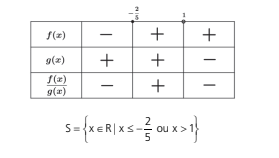
Exercício Resolvido
- (UEPB) A soma das raízes que a equação modular ||x – 2| – 7| = 6 é
a) 15
b) 30
c) 4
d) 2
e) 8
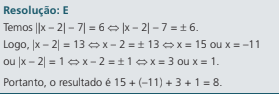
Exercício Resolvido

Exercício Resolvido

Exercício Resolvido

Exercício Resolvido




