CONCEITOS BÁSICOS
ESTATÍSTICA
É a ciência que utiliza a coleta de dados, sua classificação, sua apresentação, sua análise e sua interpretação para se tomar algum tipo de decisão.
ESTATÍSTICA DESCRITIVA
É o ramo da Estatística que se ocupa em organizar e descrever os dados que podem ser expressos por tabelas e gráficos.
ESTATÍSTICA INFERENCIAL
É o ramo da Estatística que utiliza técnicas de análise e interpretação de dados, a partir de uma amostra de uma população, e fornece conclusões sobre este conjunto.
POPULAÇÃO
Na coleta de dados sobre determinado assunto, chama-se população estatística, o conjunto formado por todos os elementos que possam oferecer dados relativos ao assunto em questão.
Podemos dizer que população é qualquer conjunto que reúna todos os elementos que tenham pelo menos uma característica comum, objeto de estudo.
AMOSTRA
É um subconjunto de uma população. A seleção da amostra pode ser feita de várias maneiras, dependendo, entre outros fatores, do grau de conhecimento que temos da população, da quantidade de recursos disponíveis e outros fatores. A seleção da amostra deve fornecer um
subconjunto de valores mais parecido possível com a população original.
Exemplo:
Uma pesquisa típica de audiência na televisão utiliza uma amostra de 5000 lares e, com base nestes dados, formula conclusões acerca de uma população de todos os milhões de lares no país.
CENSO
É o método utilizado para um trabalho com uma população.
DADOS ESTATÍSTICOS
Os dados são denominados quantitativos quando são representa- dos por números ou medidas, como por exemplo as alturas de uma população, o número de lhos e o salário bruto. Quando os dados representam contagens são discretos e quando representam mensurações são contínuos.
Os dados são chamados de qualitativos ou nominais quando são definidos por categorias tais como: cor dos olhos, sexo, nível de escolaridade, naturalidade.
AMPLITUDE DE UMA AMOSTRA
A amplitude total dos dados é a diferença entre o valor máximo e o valor mínimo da amostra.
Exemplo:
Um pesquisador, contratado pela empresa de cervejas, deseja estudar quantas cervejas por semana seus clientes bebem. A amostra com 10 clientes resultou nos seguintes números: 2, 3, 7, 1, 10, 11, 5, 2, 8, 9.
A amplitude desta amostra é igual a 11 – 1 = 10.
ROL
Os dados coletados em uma amostra podem ser organizados em tabelas ou gráficos. Para isso, antes devemos organizá-los em sequências crescentes ou decrescentes denominadas Rol.
Exemplo:
No exemplo anterior organizando em ordem crescente temos: 1, 2, 2, 3, 5, 7, 8, 9, 10, 11.
DADOS BRUTOS
Podemos considerar como dados brutos aqueles que não estão numericamente organizados.
Exemplo:
2, 3, 7, 1, 10, 11, 5, 2, 8, 9.
VARIÁVEIS
Uma outra definição que aparece na análise de dados estatísticos é o conceito de variável.
Uma variável é quantitativa quando seus valores podem ser representados por contagem (variáveis quantitativas discretas) ou mensuração (variáveis quantitativas contínuas).
Uma variável é qualitativa quando apresentam como resultado um atributo, qualidade ou preferência de um entrevistado.
SÉRIES ESTATÍSTICAS
Uma série estatística é um conjunto de dados estatísticos que fazem referência aos seguintes fatores: tempo, local e fenômeno.
Os exemplos mais comuns de séries estatísticas são:
• a série temporal, cronológica ou Hhistórica;
• varia o tempo;
• a série geográ ca, territorial ou espacial;
• varia o local;
• a série especí ca ou especi cativa;
• varia o fenômeno.
Elementos essenciais em uma tabela:
• Título – é a indicação contida na parte superior da tabela, onde deve estar de nido o fato observado;
• Corpo – é constituído por linhas e colunas, que fornecem o conteúdo das informações prestadas;
• Cabeçalho – é a parte da tabela que apresenta a natureza do que contém cada coluna.
Há ainda os elementos que complementam a tabela como, por exemplo:
• Fonte – designação da instituição que forneceu os dados estatísticos.
Exemplo:
Datafolha, IBOPE, IBGE, INPE e etc.
• Notas – esclarecimentos de natureza geral.
TABELAS DE FREQUÊNCIAS
Um processo que possibilita uma leitura mais sucinta dos dados é a construção de uma tabela de frequências.
Exemplo 1:
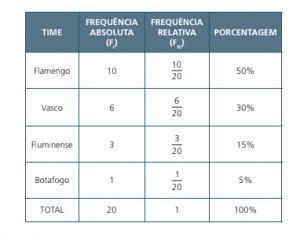
Uma entrevista com 20 pessoas é realizada no estado do Rio de Janeiro. O objetivo da pesquisa era saber qual o time do entrevistado.
Dos 20 entrevistados foram encontrados os seguintes resultados para a frequência absoluta dos entrevistados:
Flamengo (f1 = 10)
Vasco (f2 = 6)
Fluminense (f3
= 2)
Botafogo (f4
= 1)
Note que f1
+ f2
+ f3
+ f4
= 20.
Definimos frequência relativa absoluta assumido por uma variável como a razão entre a frequência absoluta e o número total de dados.
f f n ri i =
Exemplo 2:
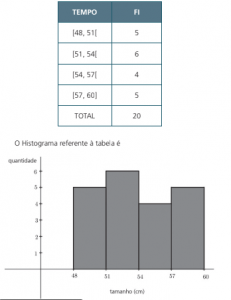
Para avaliar o tempo de permanência em um supermercado, o gerente mensurou em minutos o tempo de permanência de 20 clientes na loja. Os tempos estão representados na tabela abaixo.

Para representar esses dados em uma tabela de frequência devemos:

GRÁFICO EM BARRAS HORIZONTAIS
Os dados que estejam organizados em colunas ou linhas em uma tabela podem ser representados em um gráfico de barras horizontais.
Gráficos de barras ilustram comparações entre itens individuais.
Considere a utilização de um gráfico de barras horizontais quando:
• os rótulos dos eixos forem longos;
• os valores mostrados forem durações.
GRÁFICO EM SETORES
É utilizado quando se deseja mostrar partes do total, conforme ocorre em produções, vendas e orçamentos de países e etc.
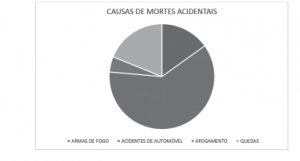
HISTOGRAMA
Quando as classes são intervalos reais, a interpretação da distribuição de frequências em um sistema de eixos é feita por um tipo de gráfico chamado Histograma.
Voltando ao exemplo 2:
POLÍGONO DE FREQUÊNCIA
O polígono de frequência é obtido unindo-se os pontos médios da parte superior de cada retângulo do histograma com segmentos de reta. É importante notar que tanto o histograma quanto o polígono de frequência indicam a frequência absoluta de cada classe. Voltando ao exemplo 2 temos:

O gráfico em linhas representativo de uma distribuição de frequências acumuladas é chamado polígono de frequências acumuladas ou ogiva de Galton. No caso de dados agrupados em
intervalos de classe, os pontos do gráfico são os pontos correspondentes aos limites superiores das classes das bases superiores dos retângulos.
CARTOGRAMA
Um cartograma é um mapa que mostra informação quantitativa mantendo um certo grau de precisão geográfica das unidades espaciais mapeadas.

PICTOGRAMA
É comum em jornais e revistas ilustrar os vários tipos de gráficos com guras relacionadas ao assunto, tornando-os mais atraentes. Esses são os pictogramas.
MEDIDAS DE CENTRALIDADE: MÉDIA ARITMÉTICA, MÉDIA ARITMÉTICA
PONDERADA, MEDIANA, MODA
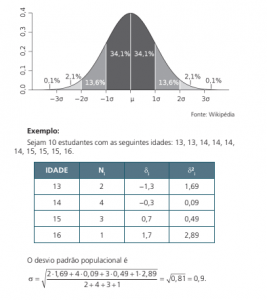
Para apresentar os conceitos a seguir, vamos considerar um grupo de 10 estudantes com as seguintes idades:
![]()
MÉDIA ARITMÉTICA E
MÉDIA ARITMÉTICA PONDERADA
Seja x uma variável quantitativa e x1 , x2 , x3 , …, xn os valores assumidos por essa variável. A média aritmética (x) de x é igual a soma de todos os valores assumidos pela variável dividida pelo número de valores, ou seja,
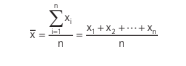

MEDIANA

MEDIDAS DE DISPERSÃO: DESVIO
MÉDIO, VARIÂNCIA, DESVIO PADRÃO
Considere uma turma de 5 alunos em que todos tiraram nota 5 e outra com a mesma quantidade de alunos com as seguintes notas: 1, 3, 5, 7 e 9. Essas duas turmas têm a mesma média aritmética e a mesma mediana que é 5. Mas a dispersão dos valores é completamente
diferente e pode ser calculado.
DESVIO MÉDIO ABSOLUTO (DMA)
O desvio em relação à média aritmética é a diferença entre cada valor e a média aritmética.

PROPRIEDADES DA VARIÂNCIA
Se adicionarmos um mesmo valor a cada um dos valores assumidos pela variável, a variância não se altera.
Se multiplicarmos cada um dos valores assumidos pela variável por um mesmo valor, a variância fica multiplicada pelo quadrado desse valor.
Se a variância for calculada sobre uma amostra em vez de sobre toda a população, teremos então a chamada variância amostral que

PROPRIEDADES DO DESVIO PADRÃO
Se adicionarmos um mesmo valor a cada um dos valores assumidos pela variável, o desvio padrão não se altera.
Se multiplicarmos cada um dos valores assumidos pela variável por um mesmo valor, o desvio padrão fica multiplicado por esse valor.