ESTÁTICA
A estática é o estudo de corpos em equilíbrio. Para analisarmos esses casos, temos que saber quais são as condições para dizermos que um corpo está em equilíbrio.
Até agora, vimos que, quando a soma das forças que atuam em um corpo é nula, este está em equilíbrio. Porém, vamos pensar em uma balança de pratos. Ao colocarmos um objeto em um dos pratos, este irá descer e o outro irá subir. Então, por mais que a balança não sofra aceleração (seu centro de massa* não se desloca), durante esse movimento dos pratos, não há equilíbrio. Supondo que o objeto foi colocado no lado direito da balança, a força peso do objeto faz com que o seu lado da balança gire no sentido horário, tirando a balança da situação de estática inicial.
A grandeza física que está intimamente ligada ao “giro” de corpos extensos, em relação a um eixo fixo, é chamada de torque (τ).
No caso da balança, quanto maior for o peso do objeto, maior será a sua aceleração angular (o “giro”).
Podemos pensar em uma gangorra de braços de mesmo tamanho. Se, do lado esquerdo, sentar uma pessoa de maior massa que do lado direito, com certeza a gangorra irá girar no sentido anti-horário. O que fazer para a gangorra permanecer em equilíbrio? Sabemos esta resposta na prática, devido a essa situação já ter acontecido com quase todas as pessoas. Basta o mais pesado se aproximar do eixo central da gangorra.
O torque depende, então, não só da força atuante, mas da sua distância em relação ao eixo. Quanto mais afastado, maior será a aceleração angular promovida (irá girar com maior facilidade). Colocar um elefante no eixo da gangorra não irá alterar o seu equilíbrio. Esse é o princípio das alavancas.
Uma observação deve ser feita. O ângulo entre os vetores força e distância é muito importante. Quando os vetores forem perpendiculares, o torque será máximo, como nos casos citados acima. Se os vetores
forem paralelos, não haverá torque. Perceba que, uma vez estabelecido o equilíbrio na situação da gangorra descrita acima, se alguém realizar uma força perpendicular ao peso, não irá fazê-la girar.

Note que, como temos um produto vetorial, o torque é uma grandeza vetorial. Perceba a diferença: ao abrirmos uma garrafa de água, temos que girar a tampa no sentido anti-horário, gerando um momento angular vertical (para saber mais, leia o aprofundamento) para cima, fazendo que a tampa suba. Para fecharmos, temos que girá-la no sentido horário, produzindo um momento angular para baixo. Qualquer porca ou parafuso funcionam com o mesmo princípio. Outra aplicação interessante no cotidiano é o ventilador de teto. Quando gira no sentido horário produz vento para baixo, e quando gira no sentido anti-horário, produz vento para cima.
Observação
O Torque também é chamado de momento da força. A origem desse termo é obscura, mas pode estar relacionada com o fato de que “momento” vem do latim movimentum e que a capacidade da força em mover um objeto (usando a força em uma alavanca) aumenta com o tamanho do braço.
Exercício Resolvido
01. Um garoto de 40 kg caminha sobre uma prancha homogênea e uniforme de 3,0 m de comprimento e massa de 60 kg. A tábua é colocada sobre dois apoios, A e B, separados por uma distância de 2,0 m. Qual a menor distância x, da extremidade livre, em cm, a que o garoto pode chegar sem que a prancha tombe?
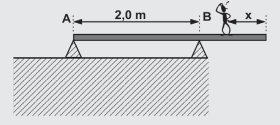
Percebemos que o peso da prancha é a força que tenta manter o equilíbrio (iminência de rotação no sentido anti-horário) e o peso do garoto é a força que tenta fazer o sistema girar (iminência de rotação no sentido horário). Se o torque causado pelo peso do garoto for, em módulo, igual ao do peso da prancha, o sistema estará em equilíbrio. Notamos também que, na iminência de girar, a tábua tende a perder o contato com o ponto A, ou seja:
Resolução:

Em que d é a distância do peso da prancha até o ponto de apoio e d’ é a distância entre o ponto de apoio e o peso do garoto. O livro não tem dimensão considerável, então d é a distância do livro até o apoio, mas qual o valor de d? Onde devemos colocar o peso em objetos extensos?
*Aí entra o conceito de centro de massa (C.M.), que veremos com maior profundidade daqui a pouco. Por hora, podemos pensar que, para corpos homogêneos, se colocarmos um apoio no seu centro geométrico, o corpo permanecerá em equilíbrio. Esse será o C.M. do corpo. Ali colocaremos a força peso.
Então, no nosso exemplo, o peso da prancha está bem na metade do seu comprimento, que está a 1,5 m da extremidade A, a 0,5 do apoio (B), logo:
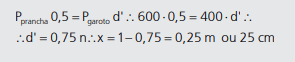
Máquinas que auxiliam o nosso cotidiano:
As principais máquinas que estão em vários livros didáticos de física são as alavancas e as roldanas. Vamos estudar cada uma dessas máquinas. Além das citadas, o plano inclinado também facilita bastante o dia a dia de muitas pessoas. Apesar de não ser uma máquina, vale a pena estudá-lo.
ALAVANCAS
Imagina uma situação-problema de milhares de anos atrás: como remover uma pedra com mais de 100 kg? Arquimedes conseguiu responder essa pergunta há mais de 2 mil anos: podemos utilizar uma barra rígida e longa, que possa girar, apoiada em um ponto. Ao colocarmos a pedra em uma de suas extremidades, conseguiremos movê-la, aplicando uma força na extremidade oposta. Esse é o princípio das alavancas.
Nesse caso, podemos dizer que a força peso da pedra é uma força resistente, pois realiza um torque no sentido oposto ao da força aplicada para tentar removê-la, chamada de força potente.
TIPOS DE ALAVANCAS
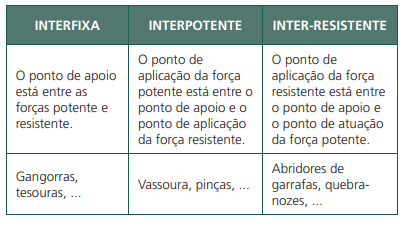
Algumas alavancas do corpo humano:
Exercício Resolvido
O C.M. de uma pedra está a 20 cm de uma pedrinha, usada como apoio para uma alavanca interfixa, conforme a figura abaixo. Qual a força que o menino deve fazer para conseguir mover a alavanca, sabendo-se que a massa da pedra vale 80 kg e que esta força está sendo aplicada a 1,0 m do apoio?
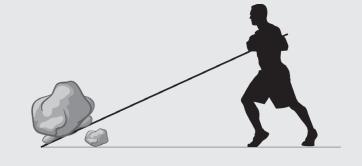
Resolução:
A força que o menino faz é a força potente. Já a força peso da pedra é a resistente. Podemos dizer que o peso da pedra faz a alavanca girar para o sentido anti-horário, e a força do menino, para o sentido oposto. Então:
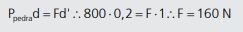
Perceba que o menino faz uma força equivalente a 1/5 do peso da pedra, ficando bem mais fácil para movê-la.
ROLDANAS
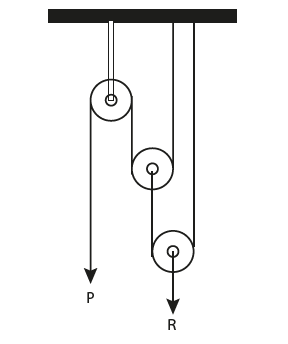
Podemos levantar objetos pesados sem o uso de muita força. Imagina uma situação na qual queremos levantar 200 kg. Como fazer isso? As roldanas podem ser a solução.
Observe a figura acima. Digamos que a força resistente (R) esteja valendo 2000 N. Note que, na figura, existem 3 roldanas, porém apenas uma está fixa no teto. Vamos chamá-la de roldana fixa. As outras duas podem se mover para cima ou para baixo. São as roldanas móveis.
Vamos isolar a roldana inferior:
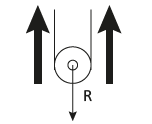
As forças que atuam na roldana (vamos considerar que a roldana não tem massa) estão representadas na figura acima. A força resistente, que é o peso do objeto a ser levantado (vamos representá-la usando a letra P, de peso), e as duas trações. Como ela está em equilíbrio:
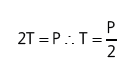
Agora vamos separar a outra roldana móvel:
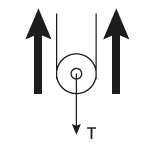
Essa roldana sofre a atuação de duas forças trações, que tendem a trazê-la para cima, e a atuação da tração do fio de baixo, que chamamos anteriormente de T, atuando no sentido oposto.
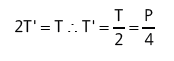
Já na roldana fixa, o fio apenas dá a volta por ela. Nada de interessante, do ponto de vista mecânico, acontece ali. Repare que a força necessária para fazer o objeto subir, com o sistema da figura, é ¼ da sua força peso. Isso acontece porque cada roldana móvel reduz a força F necessária para levantar um objeto pela metade.
No nosso exemplo, para P = 2000 N, T` = 500 N.
Para n roldanas móveis:
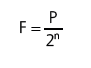
PLANO INCLINADO

As rampas ou os planos inclinados facilitam muito o transporte de carga e a vida de muitos deficientes físicos. Quanto menor o ângulo de inclinação da rampa, mais fácil será para conseguir chegar ao ponto mais alto. Mais fácil significa que é necessária uma força menor para fazer com que um objeto percorra esse desnível. Veja:
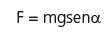
Para um sistema sem atrito, devemos aplicar uma força F para que um objeto de massa m suba um plano de inclinação x, conforme vimos em módulos anteriores. Podemos perceber que, quanto menor o ângulo de inclinação, menor o valor de F.
Para situações com atrito, a força é um pouco maior:
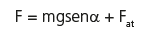
O mesmo conceito aplica-se em parafusos, brocas e serras.
TIPOS DE EQUILÍBRIO
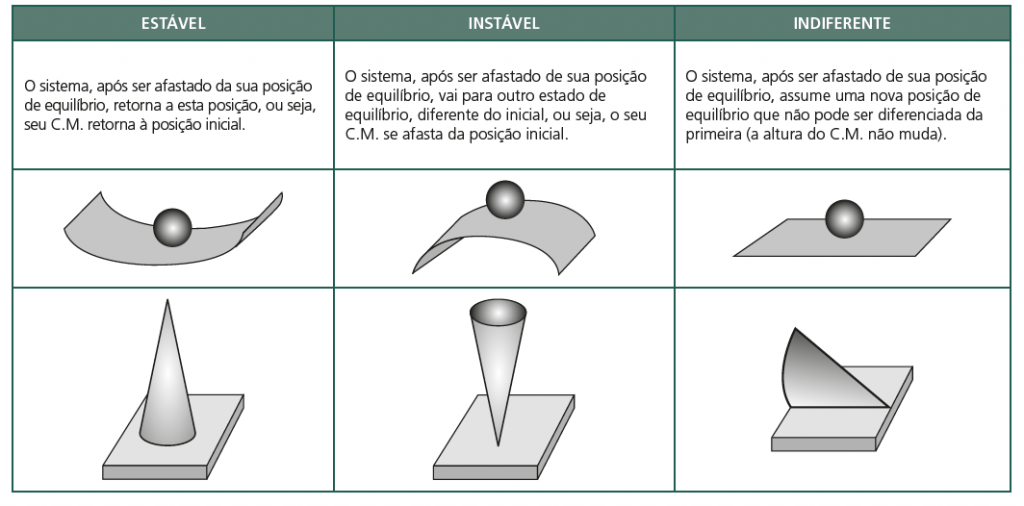
Observação
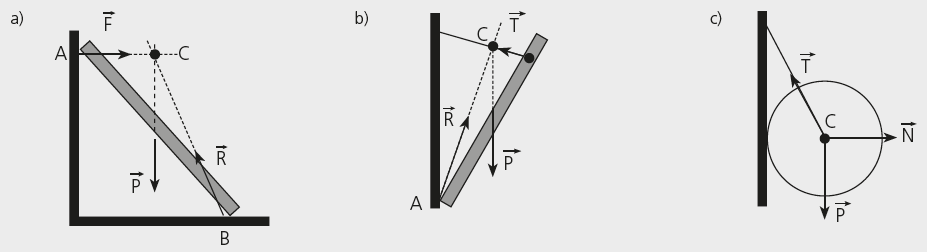
TEOREMA DAS TRÊS FORÇAS
Um corpo está em equilíbrio sob ação exclusiva de três forças. Estas deverão ser coplanares e suas linhas de forças de ação serão, necessariamente, concorrentes (a) em um único ponto ou paralelas (b).
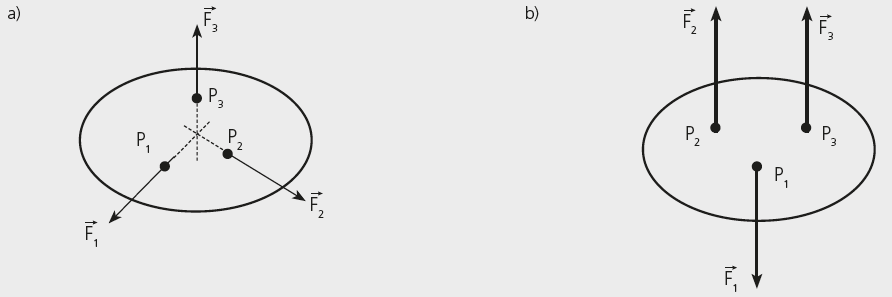
Exemplo