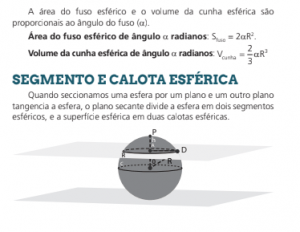
ESFERA
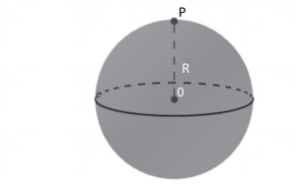
Chama-se esfera a um sólido limitado por uma superfície em que todos os pontos de um ponto interior chamado de centro. A superfície que delimita a esfera, deomina-se superfície esférica.
E qualquer segmento OP que une o centro O com um ponto P da superfície esférica denomina-se raio da esfera.
ÁREA DA SUPERFÍCIE ESFÉRICA DE RAIO R
A área da superfície esférica é igual ao quádruplo da área do círculo máximo da esfera que tem área igual a πR2 . Portanto a área da superfície esférica é S = 4πR2.

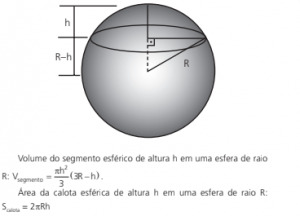
VOLUME DO SEGMENTO ESFÉRICO
De modo análogo ao volume da esfera, podemos calcular o volume do segmento esférico de altura h subtraindo um tronco de cone de altura h, de um cilindro de raio R e também altura h.
TEOREMAS DE PAPPUS GULDIN
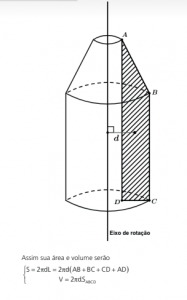
A área da superfície obtida pela rotação do arco de uma curva plana em torno de um eixo, situado no mesmo plano que a curva, mas não interceptado por ela, é igual ao produto do comprimento deste arco pelo comprimento da circunferência descrita pelo centro
de gravidade do mesmo.
Sendo d a distância do C.G. ao eixo e L o comprimento do arco, então: S = 2πdL.
O volume do corpo sólido obtido pela rotação de uma figura plana em torno de um eixo, situado no mesmo plano que a figura, mas não interceptado por ela, é igual ao produto da área desta figura pelo comprimento da circunferência descrita pelo centro de gravidade
da mesma.
Sendo d a distância do C.G. ao eixo, e S a área da gura, então:
V = 2πdS
INSCRIÇÃO E CIRCUNSCRIÇÃO DE SÓLIDOS – EXEMPLOS
Há inúmeros problemas envolvendo inscrição e circunscrição de sólidos em poliedros. Vamos mostrar dois exemplos para ilustrar, e outros estarão nos nossos exercícios de combate.
Exemplo
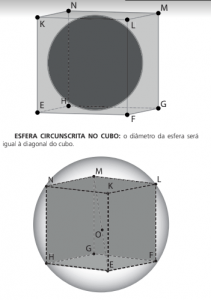
ESFERA INSCRITA NO CUBO: o diâmetro da esfera será igual a aresta do cubo.
ESFERA INSCRITA NO TETRAEDRO
REGULAR
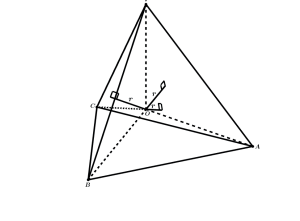
Seja uma esfera de centro O inscrita em um tetraedro regular VABC como na figura.
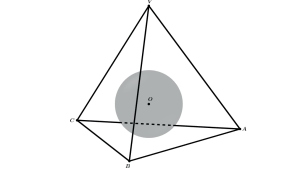
Ao traçarmos as distâncias do centro O da esfera as 4 faces VAB, VAC, VBC e ABC do tetraedro regular teremos todas essas 4 distâncias iguais ao raio da esfera (r).
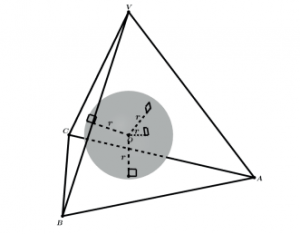
Ao ligarmos o centro O da esfera aos 4 vértices do tetraedro formaremos 4 tetraedros OVAB, OVBC, OVCA e OABC todos de alturas relativas as bases VAB, VBC, VCA e ABC iguais a r.

TEOREMAS DE PAPO-GULDINO
PRIMEIRO TEOREMA
O primeiro teorema de ne que a área de uma superfície de revolução é igual ao produto do comprimento da curva geratriz pelo comprimento do caminho percorrido pelo centroide (centro de massa) dessa mesma curva ao longo do ângulo que gera a superfície.
Ou seja, o comprimento do caminho percorrido pelo centroide é o comprimento de circunferência, assim 2π multiplicado pelo raio, que nesse caso é a distância do centro de massa ao eixo de rotação.
Assim S 2 dL = π , sendo L o comprimento da curva.
SEGUNDO TEOREMA
O segundo teorema define que o volume de um sólido de revolução é igual ao produto
da área da superfície geratriz pelo comprimento do caminho percorrido pelo centroide dessa
mesma superfície ao longo do ângulo que gera o volume.
Sendo A a área que será rotacionada, teremos de maneira análoga ao primeiro teorema V 2 dA = π .
Veja o exemplo
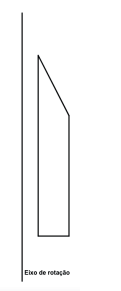
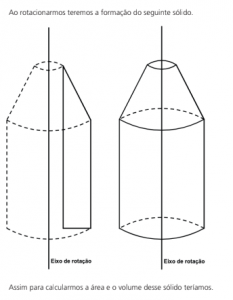
Vamos imaginar a figura abaixo sendo rotacionada em relação ao eixo de rotação
destacado.