INTRODUÇÃO
Quando um corpo sofre um aumento de temperatura, as moléculas que o compõem ficam mais agitadas (aumento da energia interna), aumentando a distância média entre as mesmas. Se sofrer uma diminuição de temperatura, a distância entre as moléculas diminui, sofrendo contração.
Os efeitos associados a esse fenômeno geralmente não são percebidos por nós, mas são levados em consideração na hora de montar uma ferrovia, por exemplo. As barras dos trilhos ferroviários são feitas com um espaçamento para não envergarem com o aumento da temperatura, ou retraírem com a sua queda.
O estudo da dilatação é dividido em três partes:
Quando uma das dimensões é muito maior que as demais, a dilatação ocorre praticamente apenas em uma dimensão, chamada de dilatação linear (o exemplo das barras dos trilhos está dentro desse tipo de dilatação).
Quando duas dimensões são bem maiores que a outra, a dilatação ocorrerá quase que totalmente nessas dimensões, chamada de dilatação superficial (uma chapa de metal, ao ser aquecida, se expande bidimensionalmente).
Observação
Alguns exercícios exploram uma situação que envolve uma chapa metálica com um buraco em seu interior. Nesses casos, quando a chapa dilata, o buraco se expande também.
A dilatação do buraco ocorre da mesma forma que a chapa dilata. É como se o buraco fosse preenchido pelo mesmo material que constitui a chapa.
Quando estamos falando de um líquido/gás, a dilatação será volumétrica, ou seja, nas três dimensões. Em sólidos cujos comprimentos das três dimensões são próximos/iguais, também ocorrerá a dilatação volumétrica.
Cada material se expande de maneira única. Dizemos que cada elemento tem o seu próprio coeficiente de dilatação. Geralmente, quando falamos de sólidos, usamos metais nos problemas, já que, nesse tipo de material, ocorre uma boa condução de calor, sendo, então, melhor observado o fenômeno. Outro fator importante para medirmos o quanto dilatará certo material é o seu comprimento/área/volume inicial. Quanto maior for, maior será sua dilatação. Por exemplo, um pedaço de ferro de 1 cm crescerá menos que outro de 1 m, se submetidos à mesma variação de temperatura. O último fator a ser analisado justamente é a variação de temperatura. Quanto maior a variação, maior será a alteração da(s) dimensão(ões) do material.
DILATAÇÃO LINEAR
Conforme mencionado anteriormente, a dilatação linear ocorre quando determinado material possui uma dimensão muito maior que as demais e sofre uma variação de temperatura.
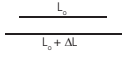
A equação que relaciona o comprimento final do material L em função da diferença de temperatura ∆T é:
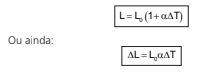
em que ∆L é a dilatação do material e α é o coeficiente de dilatação linear do material.
Exercício Resolvido
Uma régua de 1 m feita de alumínio, cujo coe ciente de dilatação linear vale 25 ⋅ 10-6 °C-1, sofre um aumento de 70 °C. Qual foi a dilatação sofrida?
Resolução:
Como a régua apresenta uma dimensão bem superior às demais, trata-se de uma dilatação linear. E como o coeficiente é menor que 10-3 °C-1, podemos usar a aproximação acima:
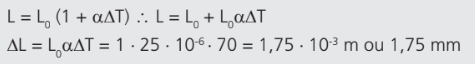
Note que a dilatação é muito pequena (0,175%).
DILATAÇÃO SUPERFICIAL
Imagine que temos uma chapa metálica retangular a x b. Como a dilatação ocorrerá nas duas dimensões, teremos que:
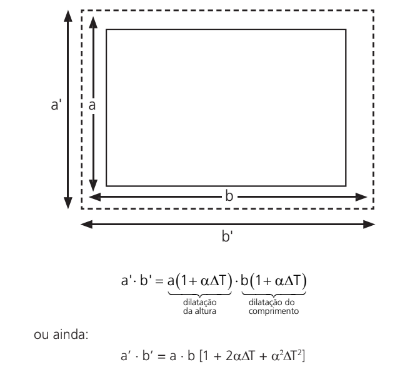
O termo α2∆T2 é muito pequeno, geralmente da ordem de 10-6. Assim, com uma boa aproximação, temos a equação da dilatação superficial do material:
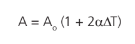
Substituindo 2α por β, o coeficiente de dilatação superficial do material, obteremos:
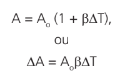
Em que A é a área final e A0 a área inicial.
Ou:

O que podemos escrever como:
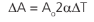
Em que β = 2α, chamado de coeficiente de dilatação superficial.
Exercício Resolvido
Uma chapa quadrada de 20 cm de lado de alumínio sofreu um aquecimento de 600 K. Qual a dilatação superficial sofrida pela chapa?
Resolução:
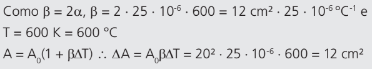
Uma variação percentual de 3% (com um aumento de 600 K).
DILATAÇÃO VOLUMÉTRICA
Para estudarmos essa última etapa, vamos imaginar um barril de alumínio contendo 10.000 litros de água. Vamos considerar que ele está completamente cheio. Entre 6 h e 14 h, sofreu uma variação de 10 °C. O que deve acontecer com o sistema?
Bom, tanto o barril quanto a água irão dilatar. Seguindo o mesmo raciocínio utilizado nos outros tipos de dilatação, conseguimos chegar na relação abaixo:

Em que γ = 3α, chamado de coe ciente de dilatação volumétrico. Vamos ver, então, qual foi a dilatação do barril:
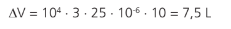
Para sabermos a dilatação da água, temos que saber o seu coeficiente de dilatação (no caso de líquidos/gases, não é necessário dizer coeficiente de dilatação volumétrico, seria um pleonasmo).
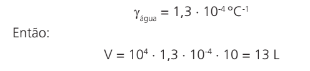
A partir dessas respostas, podemos concluir que 5,5 L de água vazaram pelo barril.



