ELEMENTOS E DEFINIÇÕES
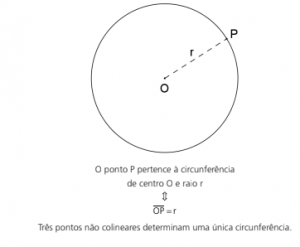
Circunferência é o lugar geométrico dos pontos do plano cujas distâncias a um ponto xo (centro) são iguais a uma constante (raio).
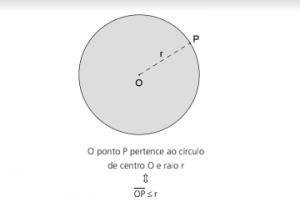
Muitas vezes, as expressões “circunferência” e “círculo” são usadas indistintamente, ora para representar a borda da gura, ora para representar a união da borda e do interior.
Corda de uma circunferência é um segmento cujas extremidades pertencem à circunferência.
Raio de uma circunferência é um segmento que possui uma extremidade no centro, outra sobre a circunferência e que tem medida constante.
Diâmetro de uma circunferência é uma corda que passa pelo seu centro. O diâmetro é a maior corda da circunferência e sua medida é o dobro da do raio.
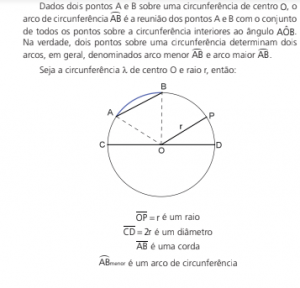
Semicircunferência é um arco de circunferência determinado por pontos diametralmente opostos.
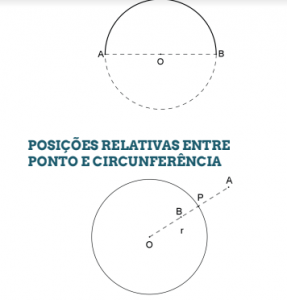

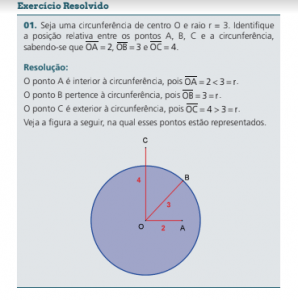
POSIÇÕES RELATIVAS ENTRE RETA E CIRCUNFERÊNCIA
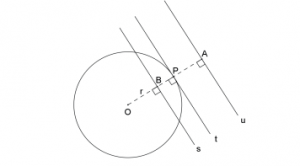
A reta s é secante à circunferência de centro O e raio r se, e somente se, a distância do centro da circunferência à reta for menor do que o raio: d(O, s) < r.
A reta t é tangente à circunferência de centro O e raio r se, e somente se, a distância do centro da circunferência à reta for igual ao raio: d(O, t) = r.
A reta u é exterior à circunferência de centro O e raio r se, e somente se, a distância do centro da circunferência à reta for maior do que o raio: d(O, u) > r.
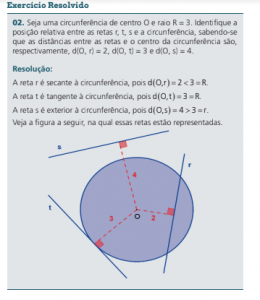
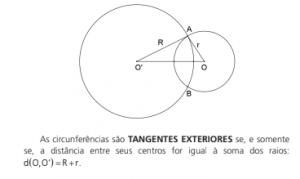
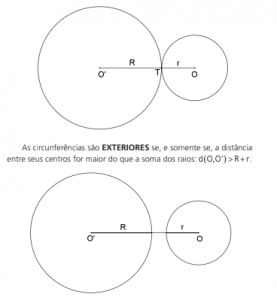
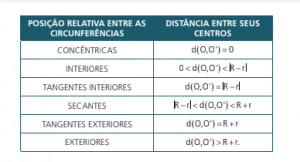
POSIÇÕES RELATIVAS ENTRE CIRCUNFERÊNCIAS
Sejam duas circunferências de centros O e O’, e raios r e R, respectivamente.
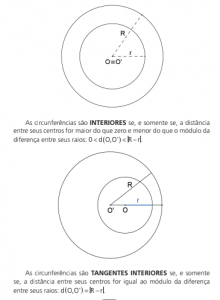
As circunferências são CONCÊNTRICAS se, e somente se, as distâncias entre seus centros for nula: d O,O’ 0

PROPRIEDADE DA SECANTE
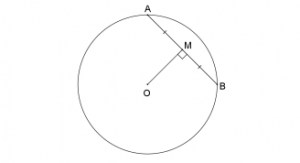
Seja uma reta s secante a uma circunferência λ de centro O e raio r, que não passa por O e que intercepta a circunferência nos pontos A e B distintos. O ponto M é o ponto médio da corda AB se, e somente se, OM AB

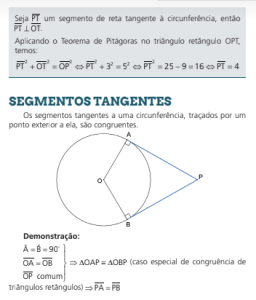
PROPRIEDADE DA TANGENTE
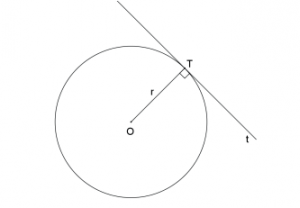
Uma reta é tangente a uma circunferência se, e somente se, for perpendicular ao raio no ponto de tangência.
Demonstração:
Seja a reta t OT ⊥ , em que T é um ponto sobre a circunferência λ de centro O e raio r. Supondo, por absurdo, que a reta t intercepta a circunferência λ em um segundo ponto P, o triângulo OTP é retângulo de hipotenusa OP e, portanto, OP > OT = r, o que implica que P é exterior à circunferência (ABSURDO). Logo, a reta intercepta a circunferência em um único ponto, ou seja, é tangente à circunferência.
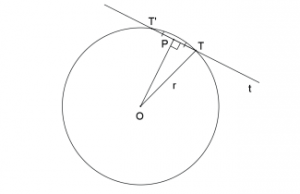
Seja t uma reta tangente à circunferência λ em um ponto T. Supondo, por absurdo, que OT é oblíqua à reta t, seja P a projeção de O sobre a reta t, então P é distinto de T. Seja T’ t ∈ o simétrico de T em relação a P, então OT OT’ r = = , o que implica que T’∈ λ (ABSURDO). Logo, OT t ⊥ .
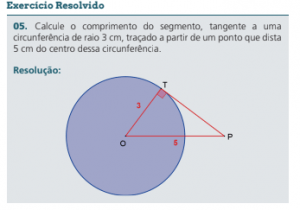
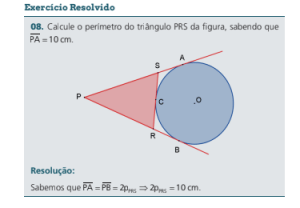
SEGMENTOS DETERMINADOS PELO CÍRCULO INSCRITO
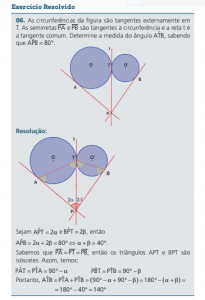
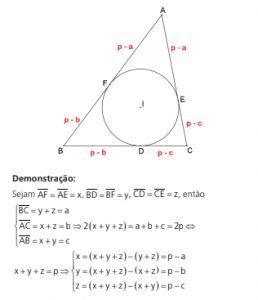
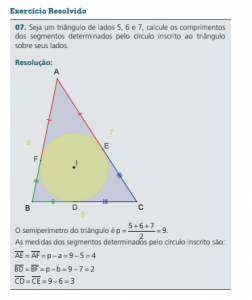
Os segmentos determinados pelo círculo inscrito sobre os lados de um triângulo têm medidas iguais ao semiperímetro menos o lado oposto.
No triângulo ABC a seguir, temos: BC a = , AC b = , AB c = e 2p = a + b + c. Os segmentos determinados pelo círculo inscrito sobre os lados são AE AF p a = = − , BD BF p b = = − e CD CE p c = = − .
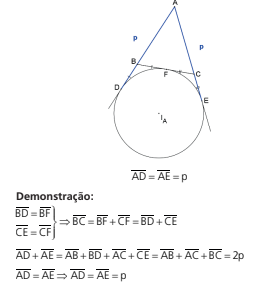
SEGMENTOS DETERMINADOS PELO CÍRCULO EX-INSCRITO
A medida dos segmentos determinados por um círculo ex-inscrito, sobre os prolongamentos dos lados adjacentes ao vértice oposto de um triângulo, é igual ao semiperímetro do triângulo.
Seja 2p o perímetro do triângulo ABC a seguir:
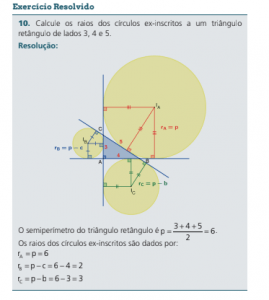
RAIO DOS CÍRCULOS INSCRITO E EX-INSCRITO AO TRIÂNGULO RETÂNGULO
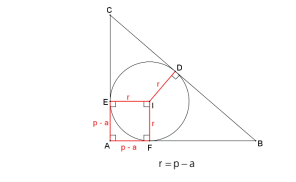
O raio do círculo inscrito em um triângulo retângulo é igual ao semiperímetro menos a hipotenusa.
Seja um triângulo retângulo ABC de hipotenusa BC a = e semiperímetro p, então o raio do círculo inscrito é r = p – a.

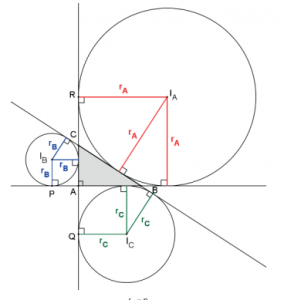

ÂNGULO ENTRE DUAS CURVAS NO PONTO
O ângulo entre duas curvas é o ângulo entre as retas tangentes às curvas nos pontos de contato.
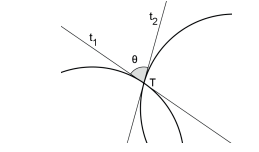
Duas curvas são ditas ortogonais se o ângulo entre elas for reto. Duas circunferências são ortogonais se, e somente se, a reta tangente a uma delas, em um dos pontos de contato, passar pelo centro da outra.
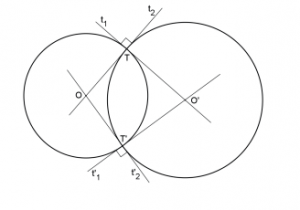
Demonstração:
Basta lembrar que a reta tangente é perpendicular ao raio no ponto de tangência.
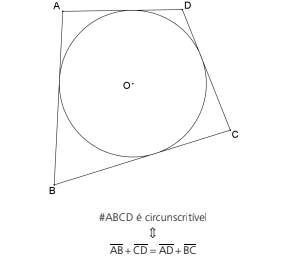
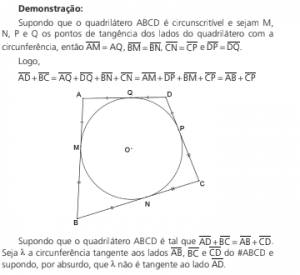
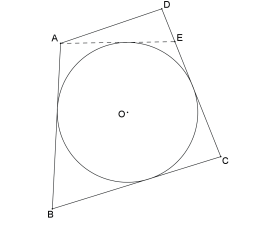
QUADRILÁTERO CIRCUNSCRITÍVEL
Teorema de Pitot: Um quadrilátero convexo é circunscritível se, e somente se, as somas das medidas dos lados opostos forem iguais.