Nesse módulo estudaremos as grandezas deslocamento, velocidade e aceleração, dando a elas o tratamento vetorial e diferenciando do tratamento escalar. Para isso temos que, inicialmente, estudar vetores e as suas operações básicas.
VETORES
Os vetores são entes matemáticos compostos de módulo, direção e sentido. Módulo é o seu tamanho (medida de comprimento do vetor), direção pode ser horizontal, vertical, e sentido, direita, esquerda, norte, sul. Com essas três informações, temos um vetor.
As grandezas físicas podem ser vetoriais ou escalares. As vetoriais precisam de todas essas informações, como: velocidade, aceleração, força, torque, entre outras. Já as escalares, só precisam de um número, como: energia, temperatura, calor, trabalho e etc.
REPRESENTAÇÃO DE UM VETOR
Além do módulo do vetor, que é o seu tamanho, temos que colocar a sua direção e o seu sentido. Para isso, vamos usar o vetor unitário, cujo módulo é 1, e indicará a sua direção. É representado pelo sinal circunflexo. O sentido virá pelo sinal.
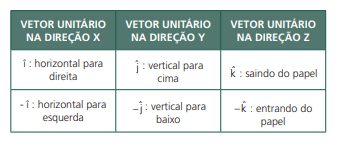
VETOR UNITÁRIO

Além dessas duas representações, podemos usar os próprios eixos cartesianos, por exemplo, e representá-lo graficamente.
Exercício Resolvido
01. Na figura abaixo temos um lançamento oblíquo.
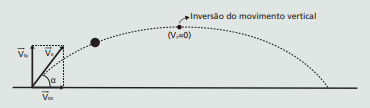
a) Qual é o vetor velocidade do projétil no instante inicial?
b) Qual é o vetor velocidade do projétil em um instante de tempo t qualquer, sendo t menor que o tempo total do movimento?
c) Qual é o vetor aceleração que o projétil está submetido?
Resolução:
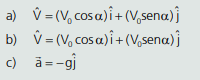
Exercício Resolvido
02. Qual é o vetor unitário na direção do vetor v = (1, –2, 4)?
Resolução:
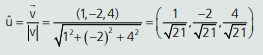
OPERAÇÕES COM VETORES
SOMA

Usando a Lei dos Cossenos:
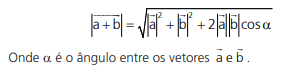
Exercício Resolvido
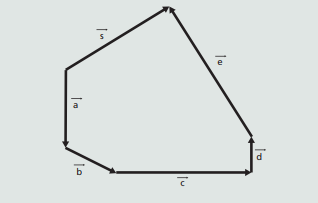
03. Qual a soma dos vetores abaixo, ou seja, qual o vetor resultante?
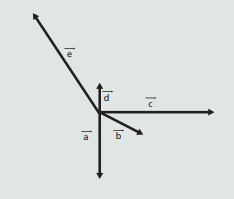
Resolução:
Veja que:
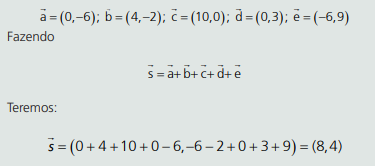
A soma é um vetor que parte da origem e ocupa 8 quadrados na horizontal e 4 na vertical, como a figura abaixo:
Note que
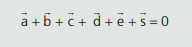
Conhecida como regra do polígono.
SUBTRAÇÃO
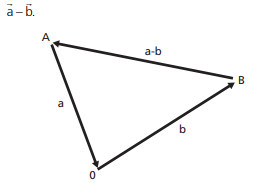
Na figura abaixo temos a representação geométrica do vetor diferença

Exercício Resolvido
04. A posição inicial de uma partícula é (0,0,2) m e a posição final é (2,0,0) m. Qual é o vetor deslocamento e qual o valor de seu módulo?
Resolução:
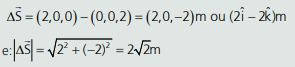
Exercício Resolvido


Resolução:
Se retorna com a mesma velocidade, em módulo, podemos inferir que o vetor velocidade final vale:
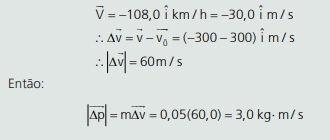
Note que, quando temos vetores em sentidos opostos, o módulo do vetor subtração será a soma de seus módulos.
Exercício Resolvido

Resolução:
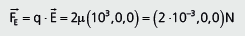
Ou seja, seu módulo vale 2 ⋅ 10–3, atua na direção horizontal e aponta para a direita. A unidade da grandeza força é N (Newton).
Observação
LEITURA OPCIONAL
A partir daqui o estudante terá contato com produto entre vetores. A leitura pode ser útil para entender com maior clareza conteúdos posteriores, como, por exemplo, as grandezas trabalho e torque.
PRODUTO VETORIAL

Observação
O produto de dois vetores dará um terceiro vetor, perpendicular aos outros dois.
Exercício Resolvido

Resolução:

O produto vetorial é o determinante da matriz:
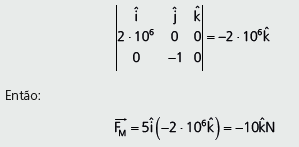
Significa que a magnitude da força magnética é 10 N e aponta para dentro da folha do exercício. Veja que esse vetor é perpendicular ao vetor velocidade, que é horizontal, e ao vetor campo, que é vertical.
Mais para frente, na próxima etapa de Física, no capítulo de força magnética, vamos aprender um método mais simples para descobrirmos desse produto vetorial, conhecido como regra da mão direita / esquerda.
Observação
O produto vetorial é zero quando os dois vetores atuam na mesma direção, ou seja, são colineares e é máximo quando osvetores são ortogonais.
Exercício Resolvido

Resolução:

Observação
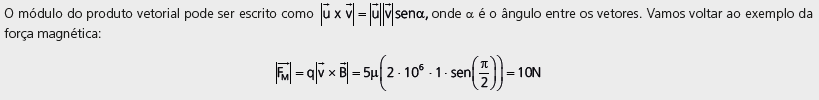
PRODUTO ESCALAR
Várias grandezas físicas são escalares, oriundas de produto escalar entre duas grandezas vetoriais.
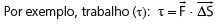
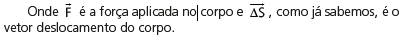
Observação
O produto escalar entre dois vetores colineares é o produto de seus módulos. Sendo assim:
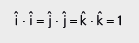
O produto escalar entre dois vetores ortogonais é zero. Sendo assim:
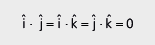
Generalizando:
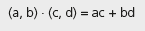
Perceba que o produto escalar é comutativo
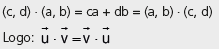
Exercício Resolvido

Resolução:
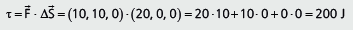
Mais tarde iremos estudar essa grandeza com mais detalhes. Mas, podemos adiantar um entendimento sobre essa grandeza. Podemos perceber que só há trabalho se a força e o deslocamento estão na mesma direção. A componente na direção ˆj não realiza trabalho (não fez nenhuma diferença no nosso exercício, pois não houve deslocamento nessa direção).
Observação

No exemplo anterior:
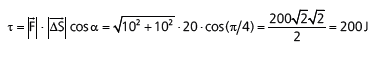
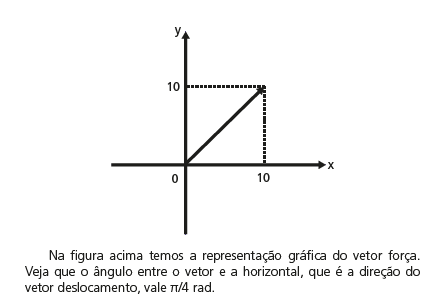
CINEMÁTICA VETORIAL
DESLOCAMENTO
Veja a figura abaixo:
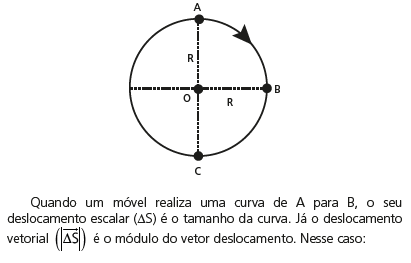
DESLOCAMENTO ESCALAR
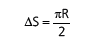
DESLOCAMENTO VETORIAL
Podemos achar o módulo do vetor de duas maneiras:
1ª: ANALITICAMENTE
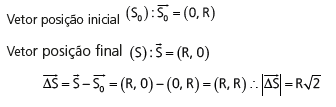
2ª: GEOMETRICAMENTE

Observação

VELOCIDADE MÉDIA

VELOCIDADE ESCALAR MÉDIA
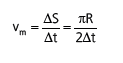
VELOCIDADE VETORIAL MÉDIA
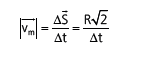
ACELERAÇÃO

ACELERAÇÃO ESCALAR
Nesse exemplo, temos que lembrar que, em uma curva, o móvel pode sofrer aceleração centrípeta e tangencial. Como a velocidade escalar é constante, não há aceleração escalar (tangencial). O fato de ser uma curva garante que o vetor velocidade (direção e sentido) muda, logo, há aceleração, a centrípeta (v²/R).
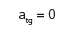
ACELERAÇÃO VETORIAL
No ponto A o vetor velocidade aponta para a direita:
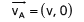
Já em B, aponta para baixo:
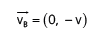
Logo:
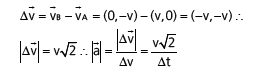
Onde v é a velocidade escalar do móvel.



