Apesar de termos estudado processos reversíveis (cíclicos), a maioria dos processos são irreversíveis. Por exemplo, um perfume, após liberado da caixa, não tende a retornar, mas expandir-se livremente, ocupando o espaço ao redor. De fato, o retorno do perfume ao frasco não viola a 1a Lei. Então, por que o gás tende a se expandir? Por que o processo é irreversível?
As tentativas de melhorar os rendimentos das máquinas térmicas tem tudo a ver com as perguntas acima. Carnot, em 1824, antes mesmo da formulação da 1a lei (meados de 40), debruçou-se diante desse problema. Seus estudos ajudaram na formulação da 2a lei de Clausius (1850) e Kelvin (1851).
ENUNCIADOS DA 2ª LEI DA TERMODINÂMICA
Kelvin: é impossível realizar um processo cujo único efeito seja remover calor de um reservatório térmico e produzir uma quantidade equivalente de trabalho.
Observação
Perceba que isso não significa que é impossível converter calor inteiramente em trabalho, como muitos autores escrevem! É possível converter todo calor em trabalho. Por exemplo, um gás em processo de expansão isotérmica. Sua variação de energia interna é zero, portanto, todo calor absorvido se converteu em trabalho (τ = Q).
Quando Kelvin disse único efeito, significa que o sistema tem que voltar ao estado inicial, ou seja, que o processo é reversível (cíclico). No exemplo acima, da expansão isotérmica, não há contradição ao enunciado de Kelvin, já que o estado inicial se difere do final. Ou seja, para processos reversíveis, considerando um ciclo completo, é impossível converter todo calor em trabalho.
Se pudéssemos ter um ciclo em que o calor se transformasse completamente em trabalho, teríamos um motor perpétuo, violando a 1ª lei. Para termos uma máquina térmica operando em ciclos, é necessário o fornecimento de calor.
Clausius: é impossível realizar um processo cujo único efeito seja transferir calor de um corpo mais frio para um corpo mais quente.
Lembrando que, novamente, aparece a expressão único efeito, ou seja, o processo deve ser cíclico. Se o gás não voltar para o estado inicial, é possível. Por exemplo, podemos colocar um recipiente contendo um gás em contato com um corpo mais frio, que pode absorver calor desse gás caso sofra um processo de expansão isotérmica (∆U = 0, Q = τ > 0). Em seguida, o gás pode sofrer uma compressão adiabática, até atingir uma temperatura maior que na etapa anterior (essa temperatura mais baixa da etapa anterior é a mesma que o corpo tem, já que estava em contato com o gás). Colocando novamente esse gás em contato com o corpo, que está a uma temperatura mais baixa que gás, o gás pode receber calor por compressão isotérmica (∆U = 0, Q = τ < 0). Nada impede que o trabalho total seja zero e o estado final seja diferente do inicial (sua temperatura aumentou) e recebeu calor de um corpo mais frio.
MÁQUINA TÉRMICA E REFRIGERADOR
MÁQUINA TÉRMICA
Pelo enunciado de Kelvin, uma máquina precisa de, pelo menos, dois reservatórios térmicos com temperaturas diferentes para funcionar em ciclos. O que possui uma temperatura maior será a fonte quente e o que possui menor temperatura, fonte fria. O gás vai absorver calor da fonte quente (vamos chamar de Qq o calor absorvido pelo gás) e irá liberar uma parte desse calor para a fonte fria (Qf será o calor liberado).
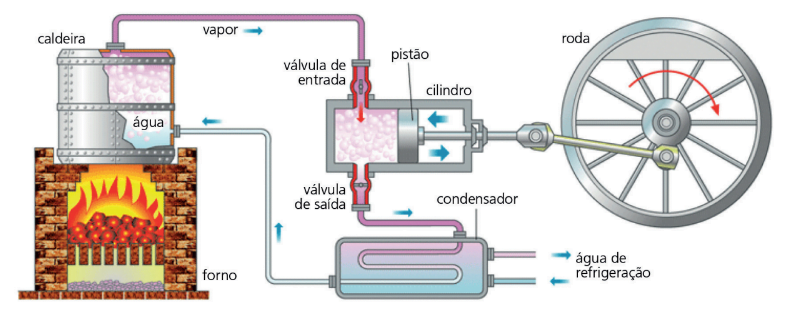
A figura anterior é um exemplo de máquina térmica. Note que é na caldeira que vapor d’água absorve calor (fonte quente) que irá impulsionar o pistão, realizando trabalho (a roda começará a girar). Veja também que a energia que o pistão não utiliza irá para o condensador (fonte fria), fazendo com que água (líquida) retorne à caldeira, reiniciando todo o processo.
O trabalho realizado é a diferença entre o calor da fonte quente e o que vai para a fonte fria:
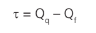
O rendimento da máquina η é calculado pela relação entre o trabalho realizado e o calor proveniente da fonte quente:
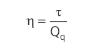
Ou, substituindo na equação acima:
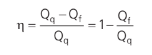
REFRIGERADOR
Numa máquina a vapor, a água é o agente. Em um refrigerador, esse agente é um líquido refrigerante, que deve ter alto calor latente de vaporização (freon, por exemplo).
O que um refrigerador faz, como um ar-condicionado ou uma geladeira, é retirar calor de um reservatório térmico frio e transferi-lo para um mais quente. O ar-condicionado, por exemplo, retira calor do quarto e joga para o meio ambiente.

Pela figura acima, podemos entender que o refrigerante remove calor da fonte fria (quarto), evaporando se, e transfere calor à fonte quente, condensando-se. Para que vaporize a uma temperatura baixa, o refrigerante tem que estar sob baixa pressão e, para que liquefaça a uma temperatura alta, deve estar sob alta pressão. Para isso, o compressor, acionado pelo motor, realiza um trabalho. Resumindo:
- o líquido a baixa pressão remove calor da fonte fria vaporizando-se no evaporador (serpentina);
- o gás é comprimido pelo compressor, aumentando a sua pressão, até se liquefazer no condensador, cedendo calor para o ambiente (fonte quente);
- para passar de líquido a alta pressão para baixa pressão, sofre uma expansão adiabática (válvula de expansão).
A eficiência (e) de um refrigerador é medida através da relação entre o calor da fonte fria e o trabalho do compressor:
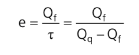
Mantendo-se a relação:
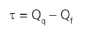
CICLO DE CARNOT
Vamos estudar, agora, como melhorar a rendimento de uma máquina térmica reversível, tarefa na qual Carnot se dedicou. Como a condução de calor é irreversível, o gás só pode trocar calor com as fontes quando estiver sob a mesma temperatura que elas, ou seja, tanto a absorção de calor (fonte quente) quanto a liberação devem ser feitas isotermicamente. E, quando o gás passar de uma temperatura para a outra, para não haver trocas de calor, essa variação deve ocorrer adiabaticamente.
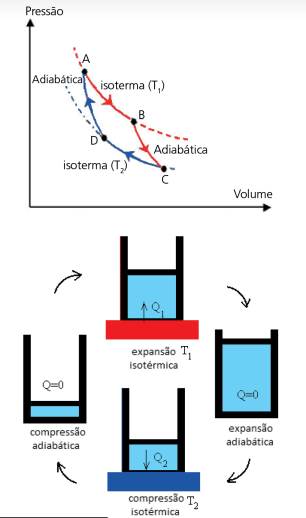
No gráfico acima, note que, como o sentido do ciclo é horário, o trabalho é positivo. Se o sentido do gráfico fosse anti-horário, o trabalho seria negativo, ou seja, remove calor da fonte fria e fornece para a fonte quente. Teríamos, então, um refrigerador.
Teorema de Carnot:
• Nenhuma máquina térmica pode ter rendimento superior ao de uma máquina de Carnot.
• Todas as máquinas de Carnot que operam entre as mesmas fontes térmicas terão o mesmo rendimento.
Vamos analisar o rendimento de uma máquina de Carnot. Usando o gráfico acima, vamos calcular calor da fonte quente (isoterma T1):
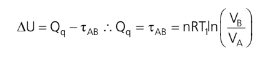
O calor cedido à fonte fria (isoterma T2) é:
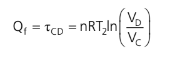
A fim de mantermos o sinal do calor da fonte fria positivo (estamos apenas considerando o seu módulo), podemos dizer que:
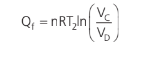

Perceba que, nem mesmo se tratando desse rendimento teórico máximo, o seu valor chegará a 100%. Para isso teríamos que ter uma fonte fria a 0K.
Para refrigerador, o cálculo de e ciência vale:
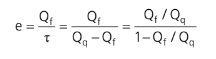
Ou seja, sua eficiência teórica máxima (Carnot) será:
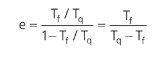
ENTROPIA, UMA ANÁLISE MACROSCÓPICA
A entropia é uma função de estado associada ao equilíbrio termodinâmico. Todo sistema tende a evoluir naturalmente para um estado de menor energia e maior entropia. Assim, como a 1a lei da termodinâmica corresponde à existência da função de estado energia interna, a 2a lei nos leva à entropia.
Para entendermos o que vem a ser essa grandeza, vamos voltar ao ciclo de Carnot. Levando o sinal negativo, do calor liberado para a fonte fria, em consideração, de modo mais correto, podemos escrever, para um ciclo de Carnot, que:
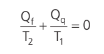
Em um ciclo reversível qualquer, como sabemos, todas as trocas de calor devem ser feitas sob temperaturas constantes. Então, podemos expandir a equação acima para qualquer ciclo reversível. Vamos chamar de dQ uma troca de calor infinitesimal. Sendo assim, obtemos o teorema de Clausius:
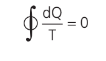
Vamos analisar o ciclo reversível abaixo:
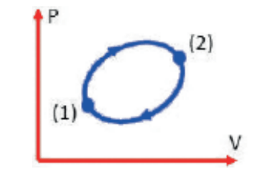
Usando o teorema de Clausius, temos que:
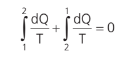
Podemos concluir que essa integral é independente do caminho. A grandeza equivalente a essa integral é, portanto, uma função de estado. É equivalente à grandeza energia potencial e energia interna. A grandeza equivalente à integral acima é a variação de entropia (∆S):
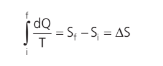
Unidade (S.I.): J/K.
Vamos aprender a calcular a variação de entropia (assim como a energia potencial, o nosso objetivo é calcular a sua diferença, e não o valor absoluto).
TRANSFORMAÇÃO ADIABÁTICA REVERSÍVEL
Como não há troca de calor nesse caso, não teremos variação na entropia do sistema.
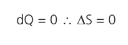
Essa transformação também é chamada de isentrópica (entropia constante).
MUDANÇA DE FASE
O que acontece com a entropia durante um processo de liquefação ou vaporização, por exemplo? Nesses casos, não há mudança na temperatura. Sendo assim:
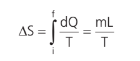
O sinal será positivo se for fusão ou vaporização, e será negativo se for liquefação ou solidificação.
Exercício Resolvido
01. Qual é a variação de entropia de 1 g de água a 100 °C, sofrendo uma vaporização?
Resolução:
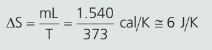
FLUIDO INCOMPRESSÍVEL
Supondo um líquido que sofresse uma variação de temperatura a volume constante. Supondo o calor específico do fluido constante durante essa variação de temperatura, temos que:
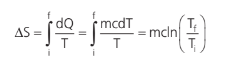
Exercício Resolvido
200 ml de água receberam calor de uma fonte quente, aumentando a sua temperatura de 20 °C para 60 °C. Qual foi a variação de entropia sofrida pelo líquido (incompressível)?
Resolução:
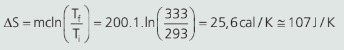
EXPANSÃO LIVRE
Como já vimos, não é um processo reversível. Para calcularmos a variação de entropia nesses casos de processos irreversíveis, como a variação de entropia só depende do estado inicial e final, seu valor será o mesmo, quer o processo que passe por esses estados seja irreversível ou reversível. Para a vizinhança do sistema, a variação de entropia não será a mesma para esses casos, mas, para o sistema em si, é.
No caso da expansão livre, podemos imaginar uma transformação isotérmica. Sendo assim:
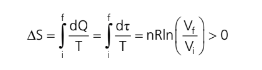
Voltando ao nosso exemplo inicial do frasco de perfume: quando destampamos o frasco, o cheiro do perfume se espalha. Como sabemos, esse processo de difusão é irreversível.
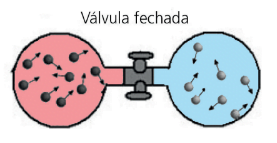
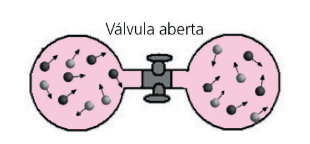
No exemplo acima, por exemplo, após a abertura da válvula, haverá uma mistura homogênea dos dois gases ocupando todo o volume possível. Podemos pensar que os dois gases sofrem expansões livres cujo volume final é o dobro do inicial. Usando a equação acima:
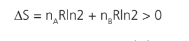
Como diferenciar o processo reversível de um irreversível apenas pela entropia? Simples, em um processo que acontece em um sistema fechado, a entropia do sistema aumenta para processos irreversíveis e fica constante para processos reversíveis. A entropia nunca diminui.
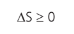
Obs.: o sistema fechado, quando levado em consideração as suas vizinhanças, chamamos de universo. É comum, em questões de concursos, considerarem que a variação de entropia de um sistema pode ser negativa, considerando sistema como um gás, por exemplo. Mas, a variação de entropia do gás mais a variação de entropia do reservatório e do ambiente ao seu redor, ou seja, a variação de entropia do universo, será sempre maior que zero.
LEITURA COMPLEMENTAR: ENTROPIA, UMA BREVE ANÁLISE MICROSCÓPICA
Os processos físicos tendem a ocorrer no sentido em que a probabilidade associada ao macroestado do sistema aumenta, tendendo ao equilíbrio termodinâmico, que corresponde ao macroestado de máxima probabilidade, ou, em outras palavras, ao macroestado de maior entropia.
Podemos definir entropia como desordem do sistema. Devemos ter muito cuidado com essa definição. Temos que saber que, quanto mais desorganizadas estiverem as moléculas, mais aleatório forem os seus movimentos, maior a entropia do sistema. O estado de entropia máximo equivale à desordem máxima, o “caos molecular”.
Vamos voltar ao exemplo da expansão livre: a probabilidade de N moléculas estarem em um volume V/2 é:
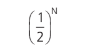
Por isso, é muito pouco provável que, após abrir a válvula, o gás que estava aprisionado na metade do volume continue ali. Imagine um gás com 1 mol de moléculas. A probabilidade de isso acontecer seria na ordem de:
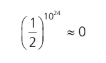
De modo geral, a probabilidade de N moléculas ocuparem um volume V’ em um espaço V é:
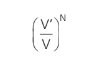
Podemos, então, calcular a relação entre as probabilidades inicial e final de um gás que se expande de um volume inicial Vi para um final Vf como:
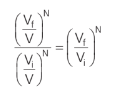
Como a variação de entropia é positiva, já que se trata de um processo irreversível, significa que o gás tende a se expandir. Quanto maior o volume ocupado pelo gás, mais microestados esse estado final terá. A relação matemática de variação de entropia em nível microscópico é:
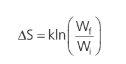
Em que W é a relação entre microestados por macroestados, chamada de multiplicidade do estado. Essa relação cará mais clara logo mais.
Ou seja, é uma probabilidade relativa, como fizemos acima. Então, no caso da expansão:
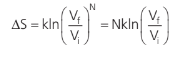
Como:
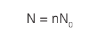
Em que n é o número de mols e N0 a constante de Avogadro.
Então:
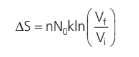
Comparando com a análise macroscópica que fizemos na expansão livre, temos que:
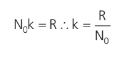
Essa é a constante de Boltzmann.
Vamos entender melhor a ideia de micro e macroestados. Veja a imagem:
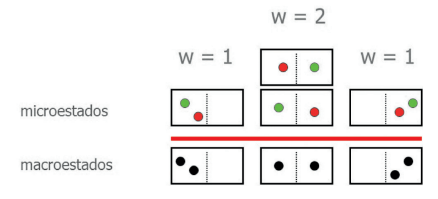
Como duas moléculas podem se organizar em uma região de volume total V, com uma fresta. Perceba que existem três macroestados diferentes: as duas no volume da esquerda, os dois na direita, ou um em cada volume. Note que existem duas maneiras de elas estarem ocupando cada volume. Ou seja, o macroestado do meio têm dois microestados.
A probabilidade de os dois ocuparem o mesmo volume é, portanto, 1⁄4. Já a probabilidade de ocuparem um cada volume é de 1⁄2. Esse é o estado com maior número de microestados, ou seja, é o estado que corresponde à tendência da evolução do sistema, o estado de maior entropia.
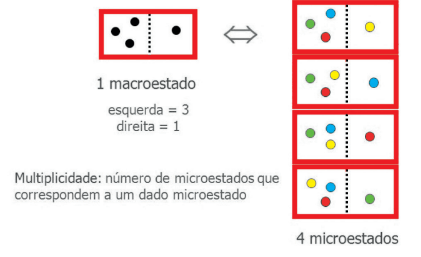
Se tivéssemos 4 moléculas, por exemplo, teríamos 16 macroestados. Os macroestados de menor probabilidade (1/16) seriam todas as moléculas na esquerda e todas na direita. O macroestado de maior probabilidade seria duas na esquerda e duas na direita. Existe 6 microestados associados a esse estado. A probabilidade de esse estado acontecer é de 6/16. Existe também a possibilidade de terem 3 moléculas na esquerda e uma na direita, ou uma na esquerda e três na direita. Para cada uma dessas situações, temos 4 microestados, logo, probabilidade de 4/16 de acontecer (1/16 + 4/16 + 6/16 + 4/16 + 1/16). Esses resultados aparecerem ao se realizar um binômio de Newton.
Quando um gás evolui de um estado para outro, podemos calcular a variação de entropia com a relação vista anteriormente.
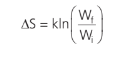
Em que Wf é a multiplicidade do estado com maior número de microestados no estado final e Wi é a multiplicidade do estado com maior número de microestados no estado inicial do sistema.



