Já discutimos sobre a lei zero da termodinâmica e as suas implicações. Agora, vamos entender o que é a energia interna de um gás, antes de chegarmos a 1a lei.
Energia interna (U): a energia interna de um gás é a soma das energias cinéticas das partículas que o compõem (como estudaremos apenas gases ideais, a energia potencial de suas partículas é zero).
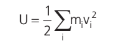
Considerando m a massa total do gás e v2 o valor médio de vi2, podemos dizer que:
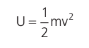
Quando um gás ideal sofre alguma transformação (como as que estudamos, por exemplo: uma compressão adiabática), poderá sofrer uma variação de temperatura. Quando as moléculas sofrem alteração de temperatura, sofrem também variação de energia cinética (basta lembrarmos que quanto maior a temperatura, maior será o grau de agitação molecular), alterando a sua energia interna.
A troca de calor de um sistema com suas vizinhanças, bem como a realização de um trabalho sobre suas vizinhanças nos dirá qual será a variação de energia interna do gás. Essa é a 1a lei:
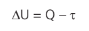
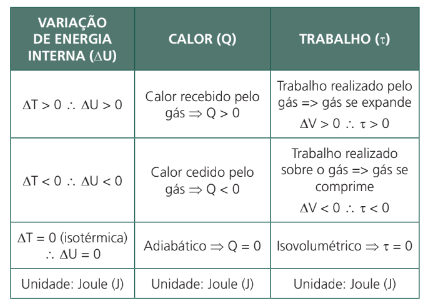
Importante nos atentarmos aos sinais das grandezas acima:
Podemos relacionar a energia interna de um gás com o grau de liberdade (N) de suas moléculas. Veja a tabela abaixo:

Lembrando que, de fato, gases diatômicos e poliatômicos não são ideais, mas vamos fazer essa aproximação, que é muito comum.
CICLOS TERMODINÂMICOS
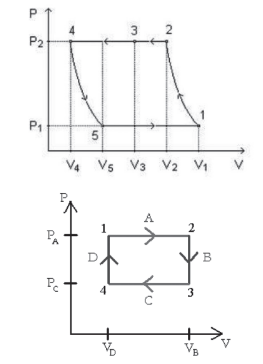
Os gráficos acima representam algumas das transformações que um gás pode sofrer. Como não existe início, meio e m, podemos ver que são transformações cíclicas.
Importante entender que a grandeza energia interna é uma função de estado. Uma função de estado é uma função que descreve uma relação entre duas ou mais variáveis de estado que de nem o estado de um sistema termodinâmico. A energia interna é definida por características das variáveis do gás no estado em que ele se encontra. Então, em um ciclo, a transformação ocorrida tem estados inicial e final iguais, então podemos concluir que:
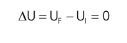
Outro detalhe importante sobre as transformações cíclicas é que o trabalho é numericamente igual à área do ciclo. Em uma transformação cíclica no sentido horário W > 0, e no sentido anti-horário W < 0.
Observação
O trabalho é uma grandeza escalar, que, em campos conservativos (campo elétrico e gravitacional), mede a variação de energia cinética de um corpo. Vimos anteriormente que é dado pela relação matemática abaixo:
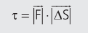
Um corpo, ao sofrer a ação de uma força F ao longo de um deslocamento ∆S, pode ganhar (τ > 0) ou dissipar (τ > 0) energia.
Quando falamos de um gás, estamos interessados em saber qual a pressão que ele exerce em um recipiente, por exemplo. Se a pressão (p) exercida pelo/sobre o gás for constante, podemos fazer a seguinte substituição:
Vamos imaginar uma seringa de área da secção transversal A, contendo certo gás no seu interior. Supondo que o êmbolo sofra um deslocamento ∆S, podemos dizer que a variação de volume do gás foi:
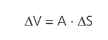
Considerando que o gás sofreu uma transformação isobárica, podemos afirmar que:
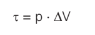
Mas, e se o gás sofrer uma transformação cuja pressão sofra variações? Nesses casos, podemos ver que, para infinitésimas variações de volume, a pressão muda muito pouco. Se tomarmos o limite onde ∆V → 0:
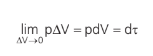
Somando cada pequeníssimo trabalho ao longo de uma transformação, teremos o trabalho total realizado/sofrido pelo gás:
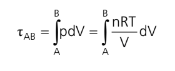
É muito comum um ciclo termodinâmico ser representado através de gráficos p x V. Note que, somando cada pdV, estamos fazendo a área do gráfico. Então, a área de um gráfico p x V é numericamente igual ao trabalho realizado/sofrido pelo gás ao longo de um ciclo.
Observação
- Se as transformações ao longo do ciclo estiverem no sentido horário, o trabalho será positivo. Se o ciclo estiver no sentido anti-horário, será negativo.
- Se o gás sofrer uma transformação isotérmica, podemos calcular com facilidade a equação acima
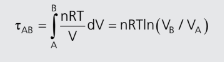
Exercício Resolvido
01. (AFA 2011) O diagrama abaixo representa um ciclo realizado por um sistema termodinâmico constituído por n mols de um gás ideal.
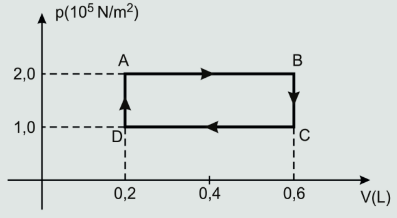
Sabendo-se que em cada segundo o sistema realiza 40 ciclos iguais a este, é correto afirmar que a(o)
a) potência desse sistema é de 1600 W.
b) trabalho realizado em cada ciclo é -40 J.
c) quantidade de calor trocada pelo gás com o ambiente em cada ciclo é nula.
d) temperatura do gás é menor no ponto C.
Resolução:
A frequência de operação é 40 ciclos/s, ou seja, 40 Hz. Notemos ainda que, no eixo das abscissas o volume está em litro. (1 L =10–3 m3). Calculando o trabalho (Wciclo) em cada ciclo. Como se trata de um ciclo no sentido horário, o trabalho realizado é positivo, sendo numericamente igual à “área” interna do ciclo.

CAPACIDADES TÉRMICAS MOLARES DE UM GÁS IDEAL
Vamos lembrar que:
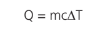
Podemos substituir a massa do gás pela expressão abaixo:
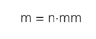
Em que n é o número de mols do gás e mm a sua massa molar. Sendo assim, podemos definir o produto da massa molar com o calor específico do gás como a capacidade térmica molar (C) do gás. Então:
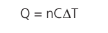
Para infinitésimas trocas de calor, teremos que:
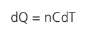
Essa capacidade térmica molar varia a depender da transformação, mas existe uma relação matemática entre a capacidade quando o gás sofre uma transformação isobárica (Cp) e a capacidade quando a transformação é isocórica (CV), que veremos logo abaixo:
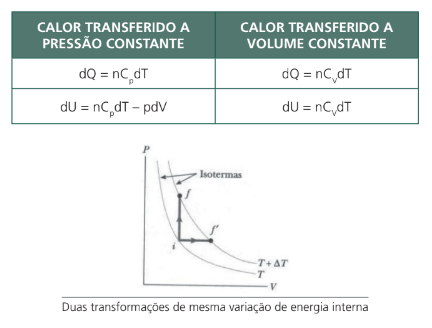
Considere a figura que representa o gráfico de uma transformação isobárica e outra transformação isovolumétrica com uma mesma energia interna, pois a energia é uma função de estado, não depende do caminho. Aplicando a 1a Lei da Termodinâmica às duas, obtemos:
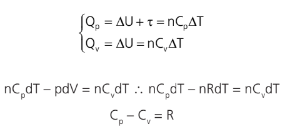
Conhecida como relação ou fórmula de Mayer.
VAMOS EXPLORAR UM POUCO MAIS SOBRE UMA TRANSFORMAÇÃO ADIABÁTICA
Nesse caso, temos que:
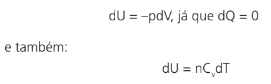
Nesse caso, o gás sofre variações de volume e pressão ao longo de toda a transformação. Como U = U(p,V):
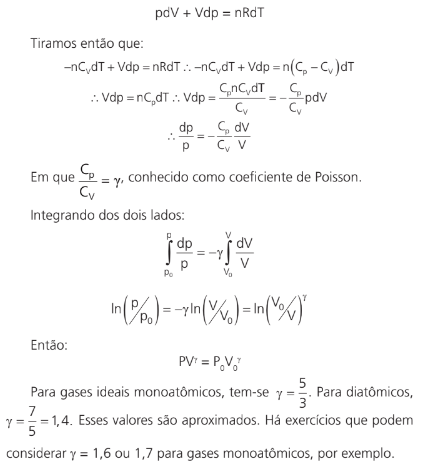
Observação
O declive de uma curva adiabática em um gráfico p × V é γ vezes n maior que o de uma isotérmica.
Poderíamos calcular o trabalho do gás em uma expansão adiabática, por exemplo. Com um pouco de cálculo chegaríamos a:
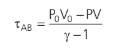
Para maiores detalhes, consultar o livro do H. Moysés, volume 02, capítulo 09.



